2009 Archives
| Dirac, Once More -- Posted by wostraub on Monday, December 7 2009 |
My
post on Michael Faraday reminded me of another story involving Paul
Dirac, which is reported in Graham Farmelo's book (see my post dated 19
November).
In his mind's eye, Faraday saw the lines of force
emanating from an electric charge or the pole of a magnet as actual
field lines in space, the flux of which in any region being directly
proportional to the field strength in that region. This view was
subsequently replaced by the field concept, which then gave way to the particle exchange concept that is used today in quantum field theory.
Dirac detested the idea of a bare electron, separate from its field, and he never accepted the technique known as renormalization,
which is used to remove the mathematical infinities associated with
bare particles in quantum field theory. In 1956, Dirac considered
Faraday's concept of lines of force and tried to reinterpret them in a
quantum-mechanical sense; that is, Dirac believed that the field lines
would become discrete in some sense when the field is quantized. Dirac
expressed this idea thusly:We may assume [that] when we
pass over to the quantum theory the lines of force become all discrete
and separate from one another. Each line of force is now associated
with a certain amount of electric charge. This charge will appear at
each end of the line of force (if it has ends) with a positive sign at
one end and a negative sign at the other. A natural assumption to make
is that the amount of charge is the same for every line of force and is
just the [size of the charge of the electron]. We now have a model in
which the basic physical entity is the line of force, a thing like a string, instead of a particle [my emphasis]. The strings will move about and interact with one another according to quantum laws. Dirac
thus anticipated string theory by several decades, and he accomplished
this by appealing to Faraday's long-discredited view of electric lines
of force.
Incredible. Edward Witten once remarked that string
theory is a bit of 21st century physics that fell into the 20th
century. By the same logic, Dirac must have come from the 25th century.
|
| Faraday's Unified Field Theory -- Posted by wostraub on Saturday, December 5 2009 |
Hermann
Weyl's 1918 theory of the combined electromagnetic-gravitational field
was an almost logical extension of the Riemannian geometry that
Einstein had relied upon when developing his own theory of gravity in
1915.
The generalization or abstraction of a successful
approach to a physical problem often meets with success, but for the
unification of gravity and other forces such as electromagnetism this
has been far from the case. Historically, Riemannian geometry has been
extended primarily via three different approaches: 1) increasing the
number of spacetime dimensions beyond four; 2) eliminating the
presumption of index symmetry in the metric tensor gμν and
associated quantities; and 3) eliminating the restriction of constant
vector length (or magnitude) under physical transplantation in
spacetime. Weyl's 1918 effort was based on the third approach, and
while it and other attempts led to interesting mathematical ideas (the
notion of torsion in tensor calculus, for example), nothing concrete has ever panned out.

Michael Faraday, 1791-1867. Copyright 2009, The Royal Society
In
view of this, it is interesting to note that the great English
physicist Michael Faraday once attempted to link gravity and
electromagnetism himself. In 1831, Faraday discovered the
electromagnetic law of induction, which states that a
time-varying magnetic field will induce a current flow in a nearby wire
(this is the basis of mechanical electrical power generation and
transformer operation). Then in 1851, noting the similarity between the
inverse-square force laws for electric charge and gravity, he
considered the possibility that a law of induction might hold for
changing gravitational fields as well. Being perhaps the greatest
experimentalist of his time, he set out to find out if there was such a
law by conducting some bench-top experiments, which he reported in a paper published by the Royal Society.
Earlier,
I posted a little story about Dirac's Large Numbers Hypothesis, in
which the ratio of the electric and gravitational forces between an
electron and proton (about 1039) plays a key role. Even in
1851, Faraday must have had at least some familiarity with this ratio,
and this awareness alone would have told him that it would be hopeless
to induce an electric current by moving fist-sized lumps of uncharged
materials (his source of gravity!) to and fro in the vicinity of a
metal wire connected to a galvanometer. But it was, conceptually at
least, an interesting experiment into the possibility that gravity and
electromagnetism might somehow be related.
And even more
interesting is the fact that Faraday's investigation preceded James
Clerk Maxwell's successful (and profoundly historic and important)
unification of the electric and magnetic fields in 1864 by a dozen
years! |
| Beautiful -- Posted by wostraub on Wednesday, December 2 2009 |
In
the 1980s I became fascinated by Mandelbrot diagrams. There were a
number of 2-D fractal computer programs at the time that allowed users
to make their own (admittedly primitive) Mandelbrot graphics under the
MSDOS operating system. The diagrams on based on a simple iterative
equation (usually involving complex numbers) that defines each point in
the graph. As iteration progresses, the points generate exceedingly
complicated figures that can be magnified infinitely.
Anyway, at
the time I wondered if such diagrams could ever be generated in 3-D,
and what they would look like. Now I know, and they're beautiful almost
beyond description:

The Cave of Lost Secrets, Copyright Daniel White 2009
The website Skytopia
(courtesy of a heads-up by John Baez' website) deserves more than a
casual look. The pictures are gorgeous, but the mathematics behind them
is perhaps even more beautiful. Skytopia also hints at the promise of
3-D video flyovers (I'm drooling now). |
| The Weylon?! -- Posted by wostraub on Sunday, November 29 2009 |
Last year saw the publication of the arXiv article Standard Model and SU(5) GUT with Local Scale Invariance and the Weylon by Hitoshi Nishino and Subhash Rajpoot. I mention this article for a number of reasons:
1.
Prior to submitting a paper, authors should always run a spell check.
Otherwise, embarrassing words like "persuits" go undetected except by
unproductive idiots like myself.
2. The article is one of
numerous papers (not all of which are available at arXiv) indicating
that Weyl's geometry (and scale symmetry) is enjoying something of a
renaissance. The above paper posits the existence of a hypothetical
vector field associated with a particle known as the "Weylon" in
conjunction with the electroweak theory. This is good, although I don't
believe such a particle exists.
3. ArXiv articles let authors get away with statements like this:

This
is also good—physicists should be allowed to express their emotions
from time to time. But Weyl's gauge idea was not in the least futile
(its 1929 resurrection is perhaps the most profound idea in physics).
And it's Hermann, not Herman, dammit.
And what kind of language is "his gauge idea may turn be out"?
Recommended
reading, but don't take it too seriously. By the way, Profs. Nishino
and Rajpoot seem to have advanced their theories to the point where
others are treading on their intellectual toes. Hence this arXiv diatribe:We
point out that the works described by Foot et al. in arXiv:0706.1829
[hep-ph] and arXiv:0709.2750 [hep-ph] are derivatives of our work
described in arXiv:hep-th/0403039, the extended version of which was
published in "Standard Model and SU(5) GUT with Local Scale Invariance
and the Weylon", AIP Conf. Proc. 881 (2007) pp. 82, Melville, New York,
2006. We are wondering how many motions (and publications!) they
will go through before finally admitting that they have re-discovered
our model, and of course, as is the usual practice these days, claiming
afterwards to the world of their independent arrival at our model.
Reference to our original work is long overdue. |
| 1039 -- Posted by wostraub on Tuesday, November 24 2009 |
Paul Dirac explains his Large Numbers Hypothesis. Audio only, undated (early 1970s); about 9 minutes.
|
| More on Dirac -- Posted by wostraub on Friday, November 20 2009 |
Farmelo's
book on Dirac is a revelation, far and away better than any other Dirac
biography available. Hermann Weyl is mentioned numerous times, although
only in connection with the early (1929-1931) debate as to whether the
negative-energy solutions of the Dirac relativistic electron equation
involved protons or some kind of new, positively-charged particle.
After discarding the proton possibility, it was Weyl who seems to have
first noticed that the new particle would have to have the same mass as
the electron. Caltech physicist Carl Anderson discovered it
experimentally in 1932, when it was named the positron—the first
particle of antimatter ever detected. It looked exactly like the
electron, but spiraled the wrong way in the detector's magnetic field.
For
students of the arcane (like me), here is Dirac's modest Tallahassee,
Florida home as it appears today, courtesy of Google Maps:

The house at 223 Chapel Drive. The Google Maps camera van caught someone mowing the lawn!
There
is also a picture of the house in Farmelo's book, evidently taken some
years ago. I wonder if the current residents are aware that a giant of
science (and perhaps the greatest physicist who ever lived) used to
reside there.
And directly across the street (at 224 Chapel
Drive) is the Chapel Hill Baptist Church. I think Dirac would have
thought it poetic in some sense, given that Wolfgang Pauli once exposed
Dirac's ambiguous religious nature with his famous quote "There is no
God, and Dirac is His prophet." |
| "I Owe Him Absolutely Nothing" -- Posted by wostraub on Thursday, November 19 2009 |
Although
I remain fascinated by the work of Hermann Weyl, my favorite physicist
has always been Paul Adrien Maurice Dirac, the theorist who discovered
antimatter and the relativistic electron equation (though Dirac once
admitted that even he could not understand Weyl).
I'm reading one of the few biographies of Dirac (and one of the even fewer good biographies), this one called The Strangest Man: The Hidden Life of Paul Dirac, Mystic of the Atom by Graham Farmelo.

Dirac was a good-looking guy, but here he looks like Tesla
In
the book's introduction, Farmelo describes how Dirac, after a lifetime
of brilliant achievement and awards, happened to leave Cambridge and
take up a research position at—of all places— Florida State University
(the stunned but elated head of the physics department noted that
getting Dirac was like the English department getting Shakespeare). He
goes on to describe how the school's top cellular biologist, Kurt
Hofer, became acquainted with Dirac and his wife, and the discussions
he had with them at the Dirac's home on 223 Chapel Drive in
Tallahassee.
The always taciturn and reticent Paul Dirac would
rarely say anything during these visits, as was his particular custom.
It was not out of disinterest, shyness or aloofness; that was just the
way he was. Hofer vividly recalls one visit in which Dirac stopped
staring at the fireplace and began to talk about his childhood in
Bristol, England. His father, a Swiss linquist, was stern and cold, and
treated his wife like a doormat and his three children the same. But
for whatever reason he insisted that his son Paul speak to him only in
French, the father's native language. And when Paul made any mistakes
in his speech, he was severely punished.

Dirac as a young child, in 1907. Sans hair, and near life's end in 1984, he looked the same!
Paul,
not particularly gifted in any language other than English, reacted by
saying nothing. He then began an uncontrolled habit of vomiting during
dinners with his father.
Hofer noted with shock how the
normally quiet and dispassionate Dirac became agitated during this
talk, but was even more shocked when Dirac added angrily "I never knew
love or affection as a child," and then, speaking of his father, burst
out contemptuously with "I owe him absolutely nothing."
Dirac's
taciturn nature has always been one of the key aspects of the lore of
Dirac, who won the Nobel prize in physics in 1933 at the age of 31. But
Farmelo's book demonstrates that there was a sad pathology behind
Dirac's "absent-minded professor" persona, one that I was not
previously aware of, and one that I now find heart wrenching in the
extreme.
I haven't finished the book yet, but so far it has
been one of the best scientific biographies I've ever read. Published
in September 2009, my local library has four copies of the book and
they're all checked out. Obviously, I'm not the only person in Pasadena
who's impressed with it! |
| How Weyl Came to America -- Posted by wostraub on Thursday, November 12 2009 |
In
1929, a wealthy American department store owner and his wife thought it
would be nice to have a renowned institute of top-notch scientists and
mathematicians to rival the great European centers of learning. So they
hired a medical administrator, Abraham Flexner, to get one for them.
Steve Batterson's Pursuit of Genius: Flexner, Einstein, and the Early Faculty at the Institute for Advanced Study
brilliantly documents Flexner's efforts to recruit the world's greatest
scientists and mathematicians and place them in the finest institute
money could buy. It's the story of how Flexner wooed the likes of
Albert Einstein, Hermann Weyl, Oswald Veblen, Kurt Gödel and others to
come to America at what turned out to be a critical time in European
history. It's also the story of how Flexner, by a combination of
salesmanship and cash, outwitted Caltech president Robert Millikan in
enticing Einstein to forgo sunny Pasadena and come instead to
Princeton.

That's Weyl in the upper left corner.
Weyl's
story is particularly interesting. By 1929, Weyl was the preeminent
mathematician at the ETH in Zürich, Switzerland, a renowned university
in its own right. But the German-born Weyl had emotional ties to
Göttingen, Germany, where he had obtained his PhD in mathematics in
1908 (at the age of 22) under the guidance of the 20th century's
greatest mathematician, David Hilbert. Zürich's climate was better for
Weyl's asthma than Germany, but with Hilbert's impending retirement
from Göttingen in 1930 Weyl was lured into taking the mathematics chair
at the famous school.
Shortly before his arrival, Weyl began
to have second thoughts. Germany's hyperinflationary problems were
still evident in 1930, and Adolf Hitler was becoming more and more
popular with the disgruntled German populace. In addition, though Weyl
was a Christian his wife was of Jewish descent, a bad heritage in the
eyes of the upcoming Nazi Party. Weyl accepted the job, but when Hitler
was appointed Chancellor in January 1933, Weyl knew his days in Germany
were probably numbered. By early April of that year, almost all of
Weyl's Jewish colleagues had been summarily fired by the Nazi regime
(of course, much worse was to follow).
However, with not one but
several invitations from Flexner to join the fledgling Institute for
Advanced Study, Weyl could not quite make up his mind to leave
Göttingen (Batterson ironically notes how Weyl could simultaneously
work on multiple mathematical problems, but could not handle the binary
problem of accepting a job!) Although his salary in Princeton would be
more than generous, Weyl worried about cultural and language issues as
well as his ongoing asthmatic condition. Just as importantly, Weyl was
a native German, and he loathed the idea of leaving his native country.
Batterson's book includes similar stories of how other notable
European scientists and mathematicians were brought together under
often trying circumstances. Though the noted American mathematical
genius George Birkhoff was one of his recruits, Flexner was concerned
about the overwhelming European (predominantly German) complexion of
the other recruits and how the new institute would suitably incorporate
these men and women into the Depression-era city of Princeton, New
Jersey.
A fascinating look at the founding of the IAS and its greatest faculty members. |
| Another Side of Weyl -- Posted by wostraub on Wednesday, November 11 2009 |
Earlier on this site I spoke of Walter J. Moore's 1992 book Schrödinger: Life and Thought, in which the rather sordid extramarital affairs (Seitensprünge,
literally, leaps to the side!) of Erwin Schrödinger and Hermann Weyl
are described. Sordid for me, but according to Moore such escapades
were no big deal in the Weimar 1920s, at least for brilliant scientists
and mathematicians.

Erwin Schrödinger, 1887-1961
Weyl
once described the 1926 discovery of the wave equation by his close
colleague Schrödinger as the result of an exceptional two-week burst of
erotic activity in the Alps, when the seemingly indefatigable
Schrödinger and an unknown lady friend desisted just long enough for
Erwin to write his Nobel-winning paper on the wave equation (which is
actually a diffusion equation, dammit).
Weyl is given
credit with assisting Erwin with the mathematics, but Weyl was not
exactly preoccupied with his work either, as he was busy with none
other than Schrödinger's wife, Anny. Indeed, though Schrödinger was a
lifelong devoted husband to Anny (he once described her as a great
friend but a lousy lover), he didn't seem to mind Weyl's adulterous
behavior, due I imagine to the liberal attitudes toward this sort of
thing as mentioned in Moore's book. And it seems that Weyl's own wife,
Hella, was herself enamored with another scientist, Peter Scherer
(sorry, I'm getting dizzy already).

Here
are just a few of the now-forgotten women involved in this sad tale. On
the left is Ithi Junger, yet another of Erwin's conquests which, if
Moore is to believed, is just one of dozens who fell under his spell.
In the middle is Hildegrund (Hilde) March, the wife of Arthur March,
another physicist colleague of Schrödinger's (Hilde was the mother of
Erwin's first out-of-wedlock child); and finally we have Anny, Weyl's
heartthrob, at least for a number of years in the 1920s.
Feet of clay, indeed. |
| Weyl and Philosophy -- Posted by wostraub on Saturday, November 7 2009 |
While
rattling off the names of numerous German philosophers in my previous
post, I did not mean to give the impression that I am at all
knowledgeable in philosophy. Quite the contrary; I find the field
fiendishly difficult, and to me the only thing more difficult than
Weyl's mathematics is his philosophy, of which he wrote extensively as
it evolved over his lifetime.

However,
so as not to give the alternative impression that I am a complete
philosophical dunce, I recently finished Simon Critchley's The Book of Dead Philosophers,
which barely covers any philosophy but instead describes how some
famous philosophers died. To me, the only real value of philosophy is
that it teaches us how to die; or, to paraphrase Montaigne, "to
philosophize is to learn to have death in your mouth." In this context,
I think Weyl would have appreciated the following words from the
introduction to Critchley's book:... what defines human life in our corner of the planet at the present time is not just a fear of death, but an overwhelming terror
of annihilation. This is a terror both of the inevitability of our
demise with its future prospect of pain and possibly meaningless
suffering, and the horror of what lies in the grave other than our body
nailed into a box and lowered into the earth to become wormfood.
We
are led, on the one hand, to deny the fact of death and to run headlong
into the watery pleasures of forgetfulness, intoxication and the
mindless accumulation of money and possessions. On the other hand, the
terror of annihilation leads us blindly into a belief in the magical
forms of salvation and promises of immortality offered by certain
varieties of traditional religion and many New Age (and some rather
older age) sophistries. What we seem to seek is either the transitory
consolation of momentary oblivion or a miraculous redemption in the
afterlife. And therein lies the crux of all our
problems: the fear of death is the motivation behind both our country's
trillion-dollar military budget and the fundamentalist Christian,
Jewish and Muslim insistence that the world become a universal
theocracy—by choice, if possible, or by force, if necessary. Just as
misery loves company, fundamentalist faith requires the uniform and
universal application of religious thought and action; does not an
inescapable ubiquity of faithful behavior make us feel that our
beliefs—which cannot, after all, be proven mathematically or
scientifically—are all real, all true? For example, the Mormon Church
strives to maintain an atmosphere or "world" in which all
entertainment, social interaction and religious activity take place
within the oversight of the church to constantly encourage the idea
that the church's teachings are true. In this sense, most of what we
call "fellowship" in the world's churches can be viewed as nothing more
than a kind of communal brainwashing in which conformity is the rule
and independent thinking is outlawed.
It is therefore
lamentable to me that Jesus Christ—man, prophet and God—today has to
preach His beautiful, unfathomable teachings on wisdom, truth, and the
love of one's fellow man under a preposterously absurd load of miracles
and other magical nonsense, so that otherwise rational human beings are
forced to struggle not only with His divine message, which is difficult
enough to live by, but with a heap of unnecessary metaphysical baggage
as well. |
| Weyl and the LHC? -- Posted by wostraub on Saturday, November 7 2009 |
At
the risk of appearing obsessive over the seeming purely metaphysical
problems of the Large Hadron Collider, and in view of the pressing need
to keep the memory of Hermann Weyl at least somewhat active on this
site (!), I'd like to quote Weyl from a manuscript he prepared in 1949
that seems curiously apropos:Here some words of Aristotle
come to mind which, to be true, refer to metaphysics rather than
mathematics. Stressing its uselessness as much as Hardy does in his
apology of mathematics, but at the same time its divinity, he says "For
this reason its acquisition might justly be supposed to be beyond human
power; since in many aspects human nature is servile; in which case, as
Simonides says 'God alone can have this privilege', and man should only
seek the knowledge which is of concern to him. Indeed, if the prets are
right and the Deity is by nature jealous, it is probable in this case
they would be particularly jealous and all those who step beyond are
liable to misfortune." (This quote also appears in Erhard Scholz' excellent article Philosophy as a cultural resource and medium of reflection for Hermann Weyl,
which explores the influence of philosophers such as Hegel, Heidegger,
Fichte and Husserl on Weyl's approach to mathematics and physics.) Of
course, I don't imagine for a moment that Weyl ever believed that some
aspects of universal knowledge are considered "off limits" by a jealous
God who acts to sabotage our efforts in protecting certain of His
secrets. Instead, Weyl goes on to what is perhaps a more realistic (if
cynical) view of mankind's scientific striving:For who can
close his eyes against the menace of our self-destruction by science;
the alarming fact is that the rapid progress of scientific knowledge is
unparalleled by a congruous growth of man's moral strength and
responsibility, which has hardly chance in historical time. The
dangers of mathematics and physics inherent in the ability of mankind
to wage modern wars (as a German, Weyl was uncomfortably close to two
of them) and to fashion weapons of mass destruction (Weyl observed with
more than a note of sadness the development of the atomic bomb and, in
1949, that of thermonuclear weapons) is indeed not in keeping with our
lagging moral progress, as Weyl asserted.
Lest one think I'm
being overly dark here, I'm not. To prove it, here's a take on the
Large Hadron Collider over at the pseudo-wiki Unencyclopedia. Enjoy, all ye who enter there.
And one more bird joke --

© Kristofer Straub, 2009 |
| For the Birds -- Posted by wostraub on Saturday, November 7 2009 |

Just when we thought it couldn't get any weirder, the European Large Hadron Collider gets shuts down by a bird dropping a piece of bread into the works. Are not two sparrows sold for a penny? Yet not one of them falls to the ground apart from the will of your Father. — Matthew 10:29
A bird! A very bird! — Humbert Humbert, Lolita At
least the LHC was not operating when the bird strike occurred, so the
planned start-up will proceed as scheduled later this month. But, given
the sheer complexity of the machine and the number of things that can
go wrong, I'm beginning to wonder if there isn't something to those claims that, if not God, then the Universe itself is sabotaging the collider from the future. Where is all this going?
|
| It Was Like That When I Got Here -- Posted by wostraub on Tuesday, October 27 2009 |
In a lecture given at Yale University in 1931, Hermann Weyl remarkedMany
people think that modern science is far removed from God. I find, on
the contrary, that it is much more difficult today for the knowing
person to approach God from history, from the spiritual side of the
world, and from morals; for there we encounter the suffering and evil
in the world, which it is difficult to bring into harmony with an
all–merciful and almighty God. In this domain we have evidently not yet
succeeded in raising the veil with which our human nature covers the
essence of things. But in our knowledge of physical nature we have
penetrated so far that we can obtain a vision of the flawless harmony
which is in conformity with sublime reason. Years earlier,
in 1919, Weyl mused over the disparity of the classical electromagnetic
and gravitational forces acting between a proton and an electron.
Noting the enormity of the dimensionless ratio of the two forces
(roughly 2.3 × 1039), Weyl suggested that it must point to
some profound meaning. As more accurate values of fundamental physical
constants became available, more and more physicists began to have the
same notion.
Then in 1937, Paul Dirac proposed his "Large
Numbers Hypothesis" (LNH), which states that all large dimensionless
numbers in nature are somehow connected. Though Dirac was a quantum
physicist, he noted that the LNH seemed to extend into the cosmological
realm as well. For example, the ratio between the age of the universe
(about 13.7 billion years) and the purely atomic unit e2mc2 (where e is electronic charge, m is electron mass, and c is the speed of light) is about 7 × 1039. Similarly, the ratio between the radius of the observed universe and the classical electron radius is roughly 1040.
Other derived ratios involve squares and cubes of this number: the
value of the cosmological constant in units of the Planck length
squared is about 10-120; the estimated number of protons in the observable universe is 1080; and the total action of the universe in terms of the Planck constant is about 10120. (Not all these figures are ratios, but you get the idea.)
In
looking over these numbers, Dirac considered two possibilities. One,
they are coincidences; and two, they result because of some conspiracy
of nature. In a 1937 paper he wroteNow, you might say, this
is a remarkable coincidence. But it is rather hard to believe that. One
feels that there must be some connection between these very large
numbers, a connection which we cannot explain at present but which we
shall be able to explain in the future when we have a better knowledge
both of atomic theory and of cosmology. Dirac's summary comments includedIt
is proposed that all the very large dimensionless numbers which can be
constructed from the important natural constants of cosmology and
atomic theory are connected by simple mathematical relations involving
coefficients of the order of magnitude unity. The main consequences of
this assumption are investigated and it is found that a satisfactory
theory of cosmology can be built up from it. Dirac's
thoughts on the LNH fueled later suppositions that at least some of the
fundamental constants of nature were changing with time. In the 1937
paper he notedLet us assume that [numbers involving the
size of the universe] are connected. Now one of these numbers is not a
constant. The age of the universe, of course, gets bigger and bigger as
the universe gets older. So the other one must be increasing also in
the same proportion. These ideas culminated in a 1973 paper by Dirac (available here), in which he examined a weakening of the gravitational constant G through an appeal to Weyl's 1918 theory of the unified gravitational/electromagnetic field.
So
if it's a conspiracy, like Dirac imagined, just what the hell is going
on? What's it all about? Does God have anything to do with it?
In 1973, the British physicist Brandon Carter came up with the anthropic principle,
which essentially states that conditions in the universe (including the
values of the fundamental physical constants) must be such that
intelligent life is possible. He further postulated that the existence
of intelligent life presupposes a "privileged" set of space-time
conditions that may exist only at certain ages of the universe. The
seeming existence of such privileged conditions has been used by many
theologians to justify the belief in God. Such an approach is largely
illusory, however, because there are alternative explanations, the most
notable being the "many worlds" interpretation of quantum mechanics and
the associated multiverse theory. But I think it might be
safe to say that there really are only three logical views: (1) The
universe and its set of physical constants are what they are because
God made them that way to make life possible; (2) The set of physical
constants is one hell of a coincidence ("it was like that when I got
here"); and (3) The number of possible multiverses (and the set of
physical constants) is infinite, and we just happen to be in one in
which life is possible ("it was like that when I got here" also applies
in this case).
Whatever or whichever is the truth (and it may
even be some combination), one has to admit that none of the above
alternative views has anything to say about the teleology of the universe, intelligent or otherwise. Teleology has to do with the ultimate purpose of things; in this sense, it is even more fundamental than the concept of driving force,
which can always be explained on the basis of non-equilibrium. I think
it really makes no sense to talk about teleology without invoking God,
because the subject is so far removed from human understanding that one
is forced to "pass the buck" on to a supernatural entity who supposedly
knows all the answers. The question "Why is there anything?"
is very much on the minds of physicists these days, and it continues to
resist all attempts at an answer. I admit that by bailing out on the
teleological aspect of all existence I am simply copping out, but I'm
pretty sure that the theologians don't know any better, either. I have
always loved asking pastors and the like questions such as 'What will
we do in Heaven? What will our purpose be there?" only to hear them hem
and haw with non-answers like "We'll just bask in God's presence, sing
songs of praise and kind of look around and admire the place." For
eternity?! Please, even God would be bored out of His mind with that.
This
brings us back to Weyl's opening remarks, in which he implies that
memorizing scripture, studying dubious (if not outright contradictory)
biblical histories and accounts, and otherwise ignoring the vast ocean
of physical and mathematical truth all around us is a colossal waste of
our God-given intellectual capabilities. I think Weyl would insist that
developing a consistent, workable theory of quantum gravity would bring
us closer to God and His plans (whatever they may be) is a far better
human undertaking than occupying our minds with nonsense such as
talking donkeys, sticks turning into snakes, parting seas, and millions
of Israelites camping out at 42 sites for 40 years in the Sinai without
leaving a single trace. And I think that when the time does come for
God to reveal His plans (we'll all have died), our souls will be in a
far better position to understand it. |
| Roy Kerr -- Posted by wostraub on Saturday, October 10 2009 |
In
1963, Cambridge-trained mathematician Roy Kerr solved a fiendishly
difficult problem in gravitational physics: the field of a massive,
rotating body. The Kerr metric describes the spacetime
surrounding a spinning black hole, a body that is in fact much more
common and natural than its non-rotating counterpart (as interstellar
gas condenses to form a star, the gas cloud's angular momentum must be
conserved, and this momentum persists throughout the star's entire
life, including final gravitational collapse to the black hole state).

Roy Kerr, 1934-
Now a book has appeared that describes Kerr's mathematical odyssey in detail for the first time. Cracking the Code: Relativity and the Birth of Black Hole Physics
by University of Arizona physicist Fulvio Melia takes us through
Einstein's field equations, the Schwarzschild description for
non-rotating bodies, and the early tentative work of Lense and Thirring
to show how Kerr arrived at his solution. While the mathematics is
minimal, the interested reader can turn to Adler, Bazin and Schiffer's
book (described elsewhere on this website) for a complete mathematical
treatment (but be warned—though elementary, it is not an easy read).
The
history of black holes is as fascinating as the subject itself. For a
variety of reasons, Einstein and many others did not believe black
holes could exist. As a star undergoes gravitational collapse at the
burn-out phase (exhaustion of hydrogen, helium and other light elements
undergoing fusion), nature intercedes against complete collapse via degenerate electron pressure,
in which the Pauli exclusion principle acts to prevent further
compression of electrons. But gravity has a way of bypassing this
pressure, and collapse of the star proceeds by fusing electrons with
protons to form neutrons. The resulting neutron star
represents the star's last bastion of hope against further collapse,
and indeed many such stars have now been observed and studied in
detail. But if the star's mass M exceeds a certain critical
amount, then no known force of nature can forestall continued
gravitational contraction; when this occurs, the star collapses to zero volume
and essentially "winks out" of existence. All that's left is a
singularity (a point of infinite density) hiding behind an event
horizon of radius R = 2GM/c2. This is the so-called Schwarzschild solution.
For
a Kerr black hole, the resulting spacetime geometry is far more
interesting. In addition to an event horizon, other surfaces arise as a
result of spacetime itself being dragged around the spinning central
singularity. Whereas the journey of a cosmonaut into a Schwarzschild
black hole is predicted to be brief and fatal, the consequences of a
similar plunge into a Kerr black hole are uncertain; the voyager may
even find herself being flung into another time or part of the
universe.
Although the mathematics of black holes are not
questioned, there are those who are still not comfortable with the idea
of a gravitational singularity, especially in view of the fact that a
quantum theory of gravitation still eludes us. The October 2009 issue
of Scientific American includes an article describing black stars,
theoretical bodies that share many of the exterior properties of black
holes but whose interiors are not singularities, just
fantastically-dense stellar cores. But such models are strictly
hypothetical, because equations of state for gases and solids of even
nuclear density are so well known today that the avoidance of complete
collapse is highly improbable.
I don't know if the mathematics of the Kerr model
have been explored by researchers to date in semiclassical gravity
theories or in attempts to formulate realistic quantum gravity
theories. Perhaps there is some kind of quantum-level phenomenon that
prevents total collapse and the formation of a singularity. But even
so, I doubt that it would rob us of the intrinsic wonder of the
mysterious object we today call a black hole. |
| Unreal -- Posted by wostraub on Wednesday, October 7 2009 |
Here is the damnedest optical illusion I've ever seen, courtesy of John Baez' website:

Are the colors (or shades) of squares A and B the same or different?
Unbelievably,
they're the same. I didn't believe it, either, so I downloaded the
picture and used Adobe Photoshop to sample A's color and compare it
with B's. They are exactly the same! I then went over to the Wikipedia site to find out why.
It
mainly involves the eye's (or rather the brain's) ability to detect
patterns in order to form meaningful images. It turns out that the eye
is not a very good light meter. Whatever.
I'm still shaking my head. |
| On the Invisibility of the Lorentz Contraction -- Posted by wostraub on Thursday, September 24 2009 |
I
got an email this morning asking me if the Lorentz contraction is
really observable. Just exactly what this has to do with Hermann Weyl
(the presumed honoré of this website) I really couldn't say,
but what I do know is that I'm no expert on Lorentz, and I tend to be
just as puzzled by it as the woman who emailed me. I wrote back telling
her to read through the back issues of John Baez' posts, as he probably explains it far better than anyone else can. But I'll share what little I know here.
I
recall a problem I had on a physics exam from long ago involving the
Lorentz contraction of a moving sphere. It is easy to prove that, in
order for light from the trailing edge of the sphere to reach the
observer at the same time as the front edge, then the light from the
back end has to have a head start. The net result is that the sphere
appears to be rotated, not contracted; consequently, a moving
sphere still looks like a sphere, and not the oblate spheroid that
might have been imagined when Einstein first wrote his famous 1905
paper on special relativity. (For the same reason, a rod moving in the
positive x-direction would appear to rotate counterclockwise about the z-axis, giving an observer the impression that it has actually contracted.)
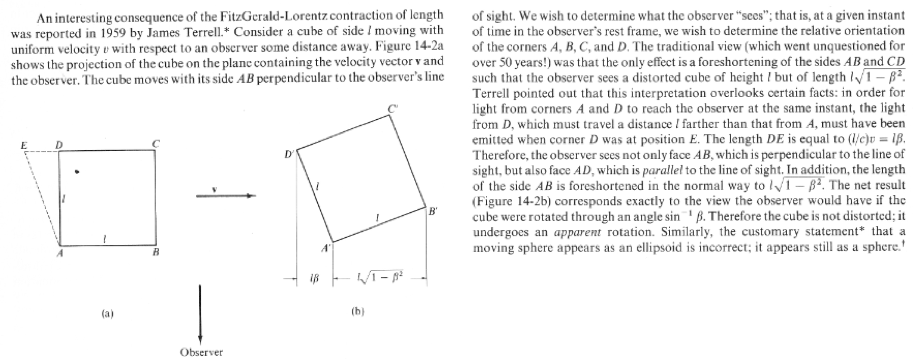
See Marion and Thornton's Classical Dynamics (1988) for a nice description of this situation
After
the exam, I asked my professor about all this. Imagining a charged
sphere with a uniform charge density, I wondered how the
electromagnetic four-vector could remain consistent with a Lorentz
transformation if the sphere remains a sphere. That is, the charge
density of a moving charged rod would contract, forcing the charge
density to increase in accordance with special relativity. A moving
sphere would not contract, so the charge density would be invariant, in
violation of relativity. The professor told me that the Lorentz
contraction is real in both cases, but you can't actually
observe it for a moving sphere. Seeing my confusion, he referred me to
a paper written by James Terrell in 1959. Well, the paper didn't help
much, and I remain confused to this day on the optical visibility of
the Lorentz contraction.
If all you need is a little elementary background on special relativity, my write-ups on the four-frequency of light and the magnetic field may be of help to you.
Anyway, here is Terrell's 1959 paper
on the visibility/invisibility of the Lorentz contraction. I re-read it
this morning, hoping that 40 years' worth of mental "maturing" would
make it an easier read for me. But no go—I still don't get it. |
| Misner - Wheeler Again -- Posted by wostraub on Tuesday, September 15 2009 |
In
response to several emails I received this morning, here's a quick
follow-up on the Misner-Wheeler "already unified" field theory I
mentioned in the last post. I will be intentionally terse because the
details are too involved. Instead, you are referred to the original
paper:
C. Misner and J. Wheeler, Classical physics as
geometry: gravitation, electromagnetism, unquantized charge and mass as
properties of curved empty space. Annals of Physics, 2:525-603 (1957).
Basically, Misner and Wheeler derived a set of conditions that must be imposed on the Ricci tensor Rμν and the contracted Ricci scalar R
for these geometric quantities to be consistent with a spacetime in
which a sourceless electromagnetic field exists; that is, it must
satisfy not only Einstein's field equations but Maxwell's equations for
the electromagnetic field. The remarkable thing about the MW theory is
that these conditions do not involve anything that looks like
electromagnetism whatsoever: the conditions are all purely GEOMETRIC!
It is in this sense that the MW theory describes gravitation and
electromagnetism as "already unified."
The MW theory assumes a
special coordinate system in which tensor indices can be ignored; the
tensor quantities in question can then all be treated as 4×4 matrices, which simplifies things enormously.
The
Einstein field equations for a source-free electromagnetic field are
given by (sorry for the crappy typesetting; I'll find something better
someday):
Rμν - ½ Rgμν = FλμFνλ - ¼ gμν FαβFαβ
If we contract both sides with gμν, we immediately get the first MW condition, which is R = 0.
Two other conditions (which I will not bother deriving here) are
R00 ≤ 0
RμνRνβ = ¼ gμβRλαRλα
The above three conditions were also derived by Rainich in 1925 using an approach different from that of MW.
MW
derived a fourth, purely-geometric condition that is too complicated
for me to express here; you'll have to read the paper if you're
curious.
The MW equations are fourth-order, highly non-linear
and difficult to solve. Wheeler suggested that in order to solve the
equations, one might introduce a fictitious antisymmetric tensor Fμν
that satisfies Maxwell's equations, use it to build a fictitious
stress-energy term, and stick this into the right-hand side of
Einstein's field equations. In this sense, the Maxwell tensor Fμν
becomes just a convenient artifice for solving the field equations. If
this view is correct (and remember that nobody has yet solved the MW
equations) then one may view the electromagnetic field tensor Fμν as a purely mathematical construct that for years has been given physical meaning!
It
is interesting to note that Hermann Weyl's 1918 gauge theory produced a
set of field equations in which the "½" coefficient in Einstein's
theory is replaced by ¼. Weyl's field equations with a sourceless
electromagnetic field energy term are therefore completely traceless,
thus eliminating the R = 0 condition.
Einstein once
remarked that the left-hand side of the gravitational field equations,
which consist of purely geometric quantities, is a beautiful
mathematical edifice that is "made out of marble," while the right-hand
side, which holds the matter and energy terms, is an ugly construct
that is "made out of wood." What he meant by this is that, while the
pure gravity terms can be derived by straightforward mathematical
arguments, there is a considerable amount of guesswork and
arbitrariness associated with the matter/energy terms. For example, one
can easily express the right-hand side for cold, catalyzed,
non-interacting matter in terms of a mass density term (no collisions,
no pressure, no gravitational/electromagnetic interaction, etc.), but
ordinary matter does not behave this way. In particular, pure matter terms have to essentially be forced
into the field equations because we don't really know where they come
from, and the interaction terms have to be guessed at. This was why
Einstein, Weyl and others had hoped that the then-new theory of general
relativity would somehow provide an explanation for the structure of
matter (and maybe even the "why" of matter).
However you may
want to look at all this, I think that the philosophical and religious
aspects of mankind's ongoing quest for the "why" and "how" of things is
profound beyond words.
The 1993 book
by Earman et al. has a nice summary of the MW unified theory, along
with those of Weyl, Einstein, Eddington, Kaluza-Klein, Mie, Cartan and
others. |
| Weyl on Matter and Singularities -- Posted by wostraub on Monday, September 14 2009 |
It
has always amazed me how quickly advancements are made to fundamental
physical discoveries. Example: In 1916, just months after Einstein's
publication of his gravity theory, the German physicist Karl
Schwarzschild used the theory to calculate the relativistically correct
description of planetary orbits, which immediately provided the
explanation for the planet Mercury's anomalous 43 arc-second
discrepancy compared with the Newtonian result. (Schwarzschild sadly
died months after his discovery from injuries received on the German
front). And in that same year, the German aeronautical engineer Hans
Jacob Reissner (1874-1967) discovered an equation similar to that
derived by Schwarzschild but describing the field of a charged mass
point. (Oddly, it took almost another 50 years for the metric of a
massive, spinning, charged object to be discovered.) Reissner was
something of an odd duck: he was not a scientist at all, but rather an
engineer who dabbled in mathematical physics; he won the German Iron
Cross in 1918 for his work in airfoil design and was highly regarded by
the Nazis in the early 1930s, but left abruptly in 1938 for a teaching
position at the Illinois Institute of Technology.
Anyway, in 1918 Hermann Weyl presented his own derivation for the metric of a charged sphere in his book Raum-Zeit-Materie (Space-Time-Matter), and he came to the conclusion that matter represents a true singularity
of the combined gravitational/electromagnetic field. Singularities in
Weyl's day were viewed with much disdain because they represented a
breakdown in the continuum view of space-time (nowadays they are still
problematic, but for a wide range of other reasons). Weyl also noted
that the then-classical view of electron structure would have to be
modified in view of the nature of this singularity, adding that it was
probably meaningless to talk about "forces of cohesion" holding the
electron together or any direct relationship between electron mass and
its surrounding electromagnetic field.
It must be remembered
that, in those early days of relativity, the nature of matter was a
preoccupation (if not outright obsession) with Weyl, Einstein and
others, and it was hoped that not only the structure of matter but the
"why" of matter might actually be describable by Einstein's physics. We
now realize how naive this hope was, if only for the fact that in 1918
just two forces — gravitation and electromagnetism — were known
(remember that this was only a few years after the "plum pudding" model
of the atom had been discarded). But the sheer beauty of Einstein's
mathematics and its interpretation in terms of space-time "warping" was
powerful and compelling, and many scientists (including Einstein and
Weyl) truly believed that a unified theory of the world was close at
hand. Well, 90 years have now gone by, and we're still waiting for that
theory!
A novel solution to the problem of singularities in the
geometry of space-time was proposed by the late, great physicist John
Archibald Wheeler and his colleague Charles Misner in 1957. Drawing
upon work done in 1925 by George Rainich, the so-called "already
unified" field theory of Wheeler and Misner is still a fun read, and
the mathematics used in its development is a joy to behold (but that is
a story I will go into another time). Wheeler dispenses with
singularities by endowing space-time geometry with a novel topology.
Imagine an empty, spherical, four-dimensional world; the introduction
of a particle of matter now does not produce a singularity but instead
produces a deformation of space-time which, according to Wheeler,
resembles a beer stein:
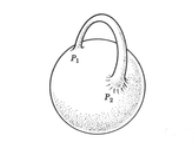
Lines of gravitational and/or electromagnetic force produced by the particle at point P1 may now flow along the handle of the beer stein and reenter the world at point P2
without the introduction of any singularity. The addition of zillions
of particles would follow the same scheme, resulting in a
four-dimensional world whose geometry resembles a Gordian knot.
Non-breaking of the associated zillions of handles might be made
physically possible by going over to spacetimes of higher dimension.
Pretty neat stuff. |
| Hermann Weyl on the Relevance of Mathematics -- Posted by wostraub on Friday, September 11 2009 |
In
his lecture given at the Princeton Bicentennial Conference in 1946,
Hermann Weyl talked about the apparent irrelevance of pure mathematics
in the real world: I have wasted much time and effort on
physical and philosophical speculations, but I do not regret it. I
guess I needed them as a kind of intellectual mediation between the
luminous ether of mathematics and the dark depths of human existence.
While, according to Kierkegaard, religion speaks of "what concerns me
unconditionally," pure mathematics may be said to speak of what is of
no concern whatever to man. It is a tragic and strange fact — a superb
malice of the Creator — that man's mind is so immensely better suited
for handling what is irrelevant rather than what is relevant to him. But Weyl went on to add that mathematics needs to be recognized as a practical tool: In
the intervals between the brain tortures of mathematical problems we
must seek somehow to regain contact with the world as a whole. The
probing of the foundations of mathematics during the last decades seems
to favor a realistic conception of mathematics: its ultimate
justification lies in its being a part of the theoretical construction
of the real world. Given the fact that Weyl gave this
lecture in 1946, the "dark depths of human existence" he refers to must
have had at least some footing in the tragic application of atomic
weapons on Japan just one year earlier. It is ironic that the seeming
irrelevance of mathematics on the real world is in fact a preposterous
misconception in this case: the atom bomb is actually a very simple
device in which two or more subcritical masses of Uranium-235 (or
Plutonium-239) are quickly brought together to create a supercritical
mass. But in order for a detonation to occur, the precise process by
which the masses are mechanically brought together (TNT implosion)
involves extremely complicated mathematics, and it was this problem
that occupied most of the mathematicians who worked on the Manhattan
Project from 1942 to 1945.

Weyl in his office, Zürich, 1927
Appropriately,
Weyl did not address this aspect of practical mathematical application
in his lecture, but instead touched on the need to recognize the purer
aspects of the field in the development of a better theoretical
understanding of the world.
Still, I think Weyl missed his
chance. He did not work on the Manhattan Project at all, preferring to
remain at the Institute for Advanced Study at Princeton to pursue more
mundane mathematical research. I have not been able to fully elucidate
Weyl's true feelings about nuclear weapons except to note that he was
far more pacifist than Edward Teller, the Manhattan Project physicist
whose abiding post-war dream was to build the "Super," the
thermonuclear fusion bomb that has now threatened the world for 60
years. But it seems very strange to me that Weyl did not at least touch
on the moral aspect of "practical" mathematics at a time when other
noted scientists, including Einstein and Oppenheimer, were left aghast
and outraged by the previous year's incineration of over 200,000
Japanese civilians. These scientists were not afraid to openly voice
their views, even when persecuted by the FBI and the House Un-American
Activities Committee.
And it is doubly strange in view of
Weyl's spiritual quests and admitted lifelong preoccupation with
philosophical issues, his love for which going back to his
post-graduate years at Göttingen.
For a dog or a mouse or a
microorganism, all mathematics is irrelevant. But for humans, math has
two primary purposes: one, to assist us in inventing the tools we need
to help us survive or improve our world; and two, to help us understand
the universe we live in. The first is indispensable, while the second
satisfies a craving that only humans can experience — the need to discover and to know.
It is an enduring sadness that for some of us — primarily the
Republicans and others of their kind wholly incapable of higher thought
— this second aspect of mathematics fulfills no purpose whatsoever.
I
freely admit that if I had never studied science, I would be an avowed
atheist today, struggling to comprehend a seemingly absurd universe
that propagates itself in accordance with undeniably beautiful physical
and mathematical laws while totally devoid of purpose. Instead, as a
consequence of my very limited understanding of science and math and,
in particular, what I know about the action principle, it is my
unwavering belief that a benevolent God exists. I would like to think
that Weyl shared these same views. |
| Hermann Weyl on Mind, Nature and God -- Posted by wostraub on Thursday, August 27 2009 |
Another rant, this time disguised as a comment on Weyl's view of God —
I
occasionally go over to Google Books to look for some book of interest.
Often, most (if not all) of the book can be read there free, although
graphics and tables usually don't come out right.
Today I was looking for Princeton University Press' new (April 2009) book on Hermann Weyl called Mind and Nature — Selected Writings on Philosophy, Mathematics and Physics, and lo and behold I found it here.
It's basically a collection of excerpts and such from some of his
longer writings, along with an informative introduction by the book's
editor, Peter Pesic. The book's only $28 at Amazon,
but since I've pretty much read everything in it already, I'll pass.
Anyway, much of what Weyl has to say in these writings deals with
philosophy and, in a roundabout way, faith.

I've never seen this picture of Weyl before.
For
whatever reason, of late I've become fascinated with Judeo-Christian
religious historicity. Although I consider myself to be a Christian, I
long ago gave up on most of the fabulous stories and miracles of the
Old Testament. They're simply ridiculous, particularly when one
compares the book's historicity with the archaeological evidence of the
past 30 years. (To see what I'm getting at, read Finkelstein and
Silberman's The Bible Unearthed: Archaeology's New Vision of Ancient Israel and the Origin of its Sacred Texts or, if you're feeling more scholarly, you can look at Donald Redford's authoritative Egypt, Canaan, and Israel in Ancient Times.
If you then still believe there was an actual Exodus event, you have my
sympathy.) My last book (it was dense and took me 8 hours yesterday to
get through the damn thing), was Lindsey's A Gathering of Saints: A True Story of Money, Murder and Deceit,
which relates the detailed story of Mark Hofmann's Mormon document
forgeries (if you know the stories behind the Kinderhook plates, the
"Book of Abraham" and Joseph Smith's seer stones, and you are still a
Mormon, then you're a complete idiot).
But, as Kelly Bundy
would say, I digest. Einstein came to terms with his Jewish religious
heritage at the tender age of 12, when he realized that many of the
Bible's stories simply could not be true. His God, as is well known,
was the God of Spinoza, indistinguishable from Nature herself. But I've
never been able to fully discern Weyl's view of God, which is not as
straightforward as Einstein's, if only because he never seems to have
come right out and said it. In some ways, Weyl's vision of God was
similar to Einstein's in the sense that Weyl viewed God not as Nature
but as "a mathematician and mathematics itself, because mathematics is
the science of the infinite" (The Open World, 1932). He also
spoke of God as the "completed infinite" (and I won't pretend that I
really understand that one). But to Weyl God was simply incapable of
being comprehended by anyone. This I understand, because I fully agree
with it.
While Weyl was shocked by the infinite capacity of
man's self-deception (and I believe he meant that in terms of most
religious belief), he seemed resigned to it, although by the time he
had turned 69 (a year before he died) he was still trying to find his
own way on the issue. As I mentioned, Einstein achieved his own peace
with religion at a very early age, and he noted later that it had much
to do with a strong sense of suspicion against authority (he once
famously remarked that as punishment for his rebellious attitude
against authority figures, God made Einstein an authority himself).
I'm
now 60 years of age, and I find that while I have come to terms with
God the Father and Jesus Christ the Savior (I am a believer but, like
Jefferson, I find it necessary as well as easy to toss out all those
silly miracles and stuff), accepting the ocean of mindless human
self-delusion that I see all around me remains frustrating in the
extreme. For example, I have nothing personal against Mormons (I worked
with a number of them, and I truly liked them), but their continued
belief in what has been proved beyond all doubt to be nothing but
preposterous nonsense demonstrates that man's dread of death and
oblivion will always outstrip his reasoning ability. I think the fact
that Utah, the Mormon's ancestral home, is the Number One Republican
state in the union, with something like an 80% approval rating for
George W. Bush, proves my point.
Not to overuse that old chestnut of Voltaire's (If you can be made to believe in absurdities, you can be made to commit atrocities),
but it's quite true. The United States was attacked on George W. Bush's
watch (he was actually more asleep than at watch), and we lost some
3,000 souls to Islamic terrorists. For the next 7 years, I watched
helplessly as terrified Americans abandoned their professed trust in
the teachings of Jesus Christ and instead embraced radical militarism,
torture and imprisonment of innocents as well as suspects, domestic
spying, and the destruction of habeas corpus and a host of
other civil liberties. Christians I thought I knew well screamed for
blood and vengence, and not a few of them advocated the nuclear
annihilation of all the Arab countries. Others were simply terrified
that we would get hit again, and as recent as this year I knew people
who would not venture into downtown Los Angeles.
But when
reminded of the apostle Paul's assertion that he would rather die and
be with Christ than go on living, all of the Christians I talked with
said something to the effect that "I am not ready to die, I still have
too many things to see and do." The hypocrisy of this attitude
absolutely astounds me — if they were truly Christians, would not God
allow them to "see and do" in the vast infinite spaces and worlds of an
eternal afterlife? Again, the subconscious dread of death overcomes
reason and the fear of future attacks becomes the rationale for the
murder, torture and abuse of fellow human beings, while religious faith
is comfortably maintained by following the advice of right-wing
monsters waving flags and Bibles.
I now feel 90% certain that
humankind will eventually destroy itself, primarily because of
differences involving nationalistic and religious antagonisms coupled
with a fervent desire to see the return of an end-times Messianic
figure. Time will tell. |
| Physics v. Math -- Posted by wostraub on Saturday, August 1 2009 |
Einstein
announced his theory of general relativity in November 1915, following
roughly four years of intense effort. A little over a year later,
Hermann Weyl was teaching a course on the subject at the Swiss Federal
Technical Institute in Zürich, and a year after that he published the
first edition of his great book Space-Time-Matter (Zaum-Zeit-Materie),
which delved far deeper into relativity than Einstein ever ventured.
Einstein did publish his own book on the subject in 1921-22 (The Meaning of Relativity), but it was vastly inferior to Weyl's in terms of depth, scope and style.
Historians
of physics know well the story of Einstein's efforts to complete his
1915 theory. What is perhaps not as well known is the fact that
Einstein was ridden with anxiety over being the first one to publish
it. The great Göttingen mathematician David Hilbert dogged Einstein
right to the very end, and in some respects it could be said that the
theory could have been called Hilbert's. It was Hilbert who, in 1915,
noticed that the gravitational field equations (which Einstein labored
to derive by way of a number of inefficient avenues), could be derived
in a matter of a few minutes's worth of scribbling using only the Ricci
scalar density and the variational principle.

David Hilbert, 1862-1943
And
it was Hilbert who, though a friend and esteemed colleague of
Einstein's, once remarked that "Every schoolboy in the streets of
Göttingen knows more about higher-dimensional geometry than Einstein,
but chalk is cheaper than gray matter."

Einstein's response to Hilbert
Indeed,
Einstein's theory was based heavily on tensor calculus, a field of
mathematics that had been developed fifty years earlier through the
work of Christoffel, Ricci, Levi-Civita and others. In his frantic
search for a coordinate-invariant theory, Einstein had turned to a
close friend (it was either Michele Besso or Marcel Grossmann), who put
Einstein onto the idea of a purely tensor formulation of relativity. It
is entirely possible that Einstein was not even aware of the existence
of tensors until sometime in 1912!
And, if the great German mathematician Bernhard Riemann had thought of the idea of basing his differential geometry in terms of four
dimensions (where the fourth dimension is time) instead of only three,
he might very well have discovered general relativity sometime prior to
1866.

Georg
Friedrich Bernhard Riemann, 1826-1866. His tragic death at 39
(tuberculosis) ended the life of the second-greatest mathematician who
ever lived (Gauss is still No. 1)
Einstein is nonetheless
given his due nowadays, by mathematicians and physicists alike. But one
should keep in mind the attitude that was prevalent with mathematicians
in the years following Einstein's publication of the 1915 theory, and
that was that physics was too important to be left to the physicists!
I
do not think that Weyl shared this view, however. Weyl is a classic
example of a "crossover" researcher who waded into physics and found an
entire new world to explore. Weyl was perhaps the first to fully
realize the great import of Einstein's discovery, and he made
fundamental contributions to the theory's advancement and extension.
Conversely, it is said that Einstein did not really like mathematics;
he once likened it to the "common enemy" of all physicists.
I
think Einstein would be totally confused by the mathematics of today's
string theory, while Weyl, I would venture to say, would at least see
the beauty if it. |
| Nostradamus and the Large Hadron Collider -- Posted by wostraub on Friday, July 31 2009 |
After
interminable delays, the European Large Hadron Collider is expected to
start up again in mid-November 2009. This event, according to a family
member of mine who will not be named here, will bring about the
planet's destruction via the creation of an uncontrollable black hole
that will swallow the Earth. On the plus side, it will also trigger The
Rapture© just prior to this catastrophe, allowing faithful Christians to join Christ in the air and escape destruction. Yay!

The "Chosen Ones" get raptured away in 2009's Knowing before this nasty event comes about. Nicholas Cage is not one of them.
How does my relative know this? Because, you see, it was predicted by the French seer Nostradamus in the 16th century. So it must be true, of course!
The
percentage of people in this country who claim to be Christians but at
the same time believe fervently in superstition, healing magnets,
dowsing rods, zodiacal astrology and the occult continues to amaze and
disappoint me. It's all a load of nonsense, but these people will only
believe what they want to believe. Besides, it takes years to learn
quantum mechanics but only two hours to read all the crap Nostradamus
ever wrote.
It's no wonder our science and math scores are so pathetic. If you can be made to believe absurdities, you can be made to commit atrocities. — Voltaire |
| The End of Einstein -- Posted by wostraub on Monday, June 15 2009 |
Albert
Einstein died on April 18, 1955 at a hospital in Princeton, New Jersey.
When admitted, he knew the end was near; he had been diagnosed months
earlier with an aortic abdominal aneurysm, and warned that he would die
when it ruptured. He was also told that his death would likely be a
horrible one.
While lying in the hospital bed, Einstein asked
for his pencil and most recent calculations. They were given to him,
and he continued working on what turned out to be his last thoughts on
Earth — a unified theory of the gravitational-electrodynamic field.
When
the end came, Einstein was in and out of consciousness. The attending
nurse reported that he muttered something in German, a language she did
not understand, then passed away. On the floor next to his bed lay
several sheets of paper, covered with calculations that looked like
gibberish to the nurse. Here is one of those sheets:

Herman Weyl would have instantly understood these calculations, as they involve a mathematical object he helped create: the coefficient of affine connection. Einstein hoped that a non-symmetrical connection term (also known as a connection with torsion) would provide a unified description of both gravitation and electromagnetism.
As
Einstein lay dying, did he dare hope that he was on the right track, or
was he merely exercising what tortured faculties he had left? We'll
never know.Linger yet, thou art so fair! — Goethe |
| Weyl and Einstein -- Posted by wostraub on Monday, June 15 2009 |
Hermann
Weyl's April 1918 metric gauge theory brought rave reviews from the
world's physicists, Einstein included. "It is a work of highest
genius," wrote Einstein to his colleague shortly after the theory's
publication. But then Einstein caught something amiss — the line
element ds of both Weylian and Riemannian geometry was
not gauge invariant, so that the lengths of all vectors would depend on
their histories. In particular, atomic spectral lines would vary from
point to point in spacetime, quite in contradiction with experience.
But
Weyl protested, indicating that God would not have missed such a golden
opportunity to embed all of electrodynamics into the geometry of the
world, as Einstein had done with gravitation. Einstein responded withCould
one really accuse the Lord God of being inconsistent if He passed up
the opportunity you discovered to harmonize the physical world? I think
not. If He had made the world according to your plan, I would have said
to Him rather reproachfully: "Dear God, if it did not lie within Thy
power to give an objective meaning to the vector equality of separated
rigid bodies, why hast Thou, Oh Incomprehensible One, not refrained
from preserving their shapes? In his communication to Weyl,
Einstein was reminding his friend that what we perceive as perfect
beauty may not be what God actually had in mind. If disproven, string
theory will certainly end up being the perfect example of such a
disconnect between our minds and God's.
Particle physicists talk
about something called "broken symmetry," which can allegorically be
taken to mean that perfect beauty sometimes has to step aside so that
the physical world can actually occur (for the mathematical details,
see my write-up
on Weyl and Higgs Theory). For example, think of the "punt" of a wine
bottle, the symmetrical hill of raised glass on the bottom that results
from the manufacturing process. Now imagine a marble balanced at the
very top of this punt. It's a perfect symmetry, but a fragile one —
equilibrium demands that the marble roll down the side and spoil
everything.
I see this also as an example of the world God made
for us. The birth of a newborn child is conceptually beautiful, but the
actual process of birth (not to mention what brought it about nine
months earlier) is a rather sticky, ugly mess.
It also serves
to disprove the prettified worldview of conservatives, who see the
world and its problems strictly in black-and-white, good-and-evil
terms. Instead, God painted the universe in grey tones, a fact that
seems to have eluded the country's Republicans. |
| Jean-Lou Chameau on American Science -- Posted by wostraub on Saturday, June 13 2009 |
Jean-Lou
Chameau is Caltech's 8th president, a French civil engineer who's
interested in earthquakes (S. California is a good place to study
them). He was interviewed recently by the Los Angeles Times, of which the following is a portion:
America
generates some of the most important science in the world, and yet many
Americans don't believe in evolution, are skeptical of science. How do
you explain this paradox?I do not know — I don't have a
background in sociology. But if you look at the major universities and
research, there is no doubt that we have the greatest work. On the
other hand, we have a K-through-12 system where, for some reason,
either science is not valued enough or it is not well communicated to
the students. So you have a significant majority of the public that has
a relatively limited knowledge of science, and it may also be afraid of
it because it was not really a major part of the education. And we are
always afraid of the unknown. The issues that are facing us — energy,
global change, health, water — science and technology are key to all
those solutions. But when we need it most, we have a large segment of
the population with limited knowledge of them. Alas, all
too true. He could also have been asked how American
science/mathematics could ever compete with Twitter, Facebook, MySpace,
American Idol and Carrie Prejean, but we all know the answer: it can't. Ignorance can be fixed, but stupidity is forever.
My
favorite retort from the conservative anti-evolutionists is that
evolution is just a theory. I tell them quantum mechanics, gravitation,
thermodynamics and electrodynamics are also just theories, but it's
these theories that drive their world. And if nuclear physics is also
just a theory, why does America base its global security on 10,000
theoretical thermonuclear weapons?
I also tell them that there
are no laws in science — it's theory all the way down. But if America's
moronic 43rd president could convince them that 1 + 1 = kat, how on Earth are they ever going to learn the truth? |
| Rosen Again -- Posted by wostraub on Monday, June 8 2009 |
A
few posts ago I related efforts I'd made to get a 1982 paper by Nathan
Rosen ("Weyl's Geometry and Physics"), as abstracts of the paper
promised a novel new approach to the Weyl-Dirac theory. Thanks to my
local library's inter-library loan program, I received the reprint
today. I've converted it into a pdf file here for those who may want to read it themselves.
It's an easy read, even if it is a trifle long at 36 pages. Rosen seems to have borrowed heavily from Adler-Bazin-Schiffer's book, at least in terms of notation and style, although he doesn't reference it. Otherwise, Rosen's approach is very original.
Like
Dirac, Rosen approaches the problem of non-integrability of vector
length by using a subterfuge that's actually better than the one Dirac
devised. Basically, Rosen redefines the Weyl affine connection for both
contravariant and covariant vectors and combines them into a new
connection that produces conformally invariant scalar, vector and
tensor quantities. And like Dirac again, he uses a variation of the
Weyl-Dirac action Lagrangian to show that the Newtonian gravitational
constant G might indeed vary inversely with universal time.
It was Dirac's original idea to produce a theory in which G
gets weaker as the universe gets older. Long ago, Dirac had noticed
that the magnitudes of certain dimensionless ratios (like that of the
electric to the gravitational force between the electron and proton)
appeared again and again in certain mathematical expressions he was
playing around with. Sensing this could not be a coincidence, Dirac was
subsequently led to believe that this could only be the case if the
gravitational constant varied slowly with time.
Dirac could
not adequately explore this idea using Einstein's theory of general
relativity because Einstein's theory presupposes that G is a
true constant. In 1973, Dirac turned to Weyl's original 1918 gauge
theory and found it was much better suited to his purposes. Rosen
references Dirac's paper, which I had posted here several years back.
It's well worth wading through. |
| Idiot America -- Posted by wostraub on Saturday, June 6 2009 |
I just finished reading Bart Ehrman's Jesus, Interrupted and Charles Pierce's Idiot America.
Pierce's book is a bit of a rant, but it speaks the truth and is
enormously entertaining as well. Conversely, Ehrman is a highly
respected Bible scholar who has published extensively on the provenance
of the New Testament gospels and epistles. I've now read a total of
three of his 20 or so books.
The commonality between these two
books involves human reasoning or, more accurately, non-reasoning.
Pierce proposes that in America today we have created and embraced a
belief system that is based on hucksterism and entertainment, not facts
or truth. By comparison, Jesus, Interrupted examines the
fallacies behind the true authorship of the New Testament and why we
believe what we believe irregardless of the historical facts.
There
is an old Arab proverb that says when God made us humans, we
immediately began to complain about our supposed physical imperfections
(our ears and noses are too big, etc.). But the one thing we are
completely satisfied with is our minds and the way we think — we're all
perfectly happy with our thought processes and the validity of our
belief systems. How many of us has said "I wish I had the same opinions
as my neighbor"?
Sadly, Americans have reached the point where they can no longer reason anymore.
Pierce states that he was motivated to write his book after visiting the Creationism Museum in Petersburg, Kentucky, which is the work of a group called Answers in Genesis. When he saw the throngs of people attending the museum, which features a life-size fiberglass Triceratops
outfitted with a saddle (proving that humans and dinosaurs had
coexisted 6,000 years ago), he knew he had to address just how idiotic
Americans had become.

Was Jesus 30 feet tall, or is this a mini-Diplodocus?
I
myself thought I had seen it all, but now I learn that the AiG people
have explained dinosaur fossils as either the work of Satan (to deceive
us) or God (to test our faith). They now readily admit (albeit
reluctantly) that dinosaur fossils are real, and that radiometric
potassium-argon dating methods are accurate. But they insist that we
mustn't believe our own eyes and the results we behold, lest the
Tempter succeed in deceiving us, or God be disappointed that our faith
is weak. I guess this explains why Satan was "walking up and down" in
the Earth in the Old Testament book of Job — he was planting fossils!
[For a wonderful overview of radiometric dating from a Christian perspective, see this article by Dr. Roger Wiens, a Los Alamos physicist.]
Pierce
claims that there are two types of eccentric folk in America: the
harmless, lovable crank and the dangerous con artist. The con artists —
the Hannitys, the Limbaughs, the O'Reillys, the AiG people, the Bushes,
the Cheneys and their ilk — have won over America because Americans
have dumbed themselves down to the point of utter stupidity.
Ehrman
reaches the same conclusion but is loathe to admit it. Examples: Why do
people believe that Matthew (a tax collector), and Peter (a fisherman),
along with the other apostles, all illiterate, uneducated,
Aramaic-speaking men, could write so brilliantly in the Greek language?
And why is it that all the New Testament books and letters we have
today are copies of copies of copies of copies written hundreds of
years after Christ was crucified? Ehrman provides innumerable other
examples of why the New Testament is largely a human book. It may
indeed have been inspired by God, but the nearly uncountable omissions,
additions and modifications contained in the New Testament indicate
that God had no intention of preserving His words. If He did, He
wouldn't have left it up to us errant humans.
And Ehrman does
not neglect the Old Testament. For example, in Psalm 137 the writer
(presumed to have been Asaph, or David, or even Solomon) claims that
the smashing of Babylonian infants against rocks brings happiness. Now,
did God inspire this pornographically-awful thought, or was it just the
later musing of a vengeful, intertestimental Jewish scribe still pissed
off over Israel's defeat by the Babylonians in 586 BC? Much of the Old
Testament is nothing more than a protracted bloodbath. I find it hard
to believe that God could have ever been so heartless toward His
creation.
I am a Christian, primarily by choice. Much of what
the Bible says makes sense to me, while a lot of it doesn't. I believe
that by giving us sentience and free will, God had to provide a means
of salvation for us, which is Jesus Christ. But I engage this belief
out of choice, not because of what some authority tells me to
believe. And my belief does not give me the right to physically
threaten others for believing otherwise, or to encourage my political
leaders to invade, occupy or nuke non-believing nations.
As
Ehrman points out in his book, the Bible has to be read horizontally
(by simultaneously comparing the books in detail) as well as vertically
(one book at a time). Most Christians don't do this; in fact, they
don't even read the Bible — they peruse it. And they generally aren't even aware that other writings even exist. What kind of belief system is this?
By
dumbing ourselves down to the extent we have, we've chosen to ignore
the real proof of God's existence and benevolence — His creation of the
universe and all its laws — and instead have elected to rely on our
very imperfect thought processes and nonsensical belief systems.
Like
Pierce warns at the end of his book, things don't look good for us
unless we make some changes. And I really don't see that happening. |
| Nathan Rosen -- Posted by wostraub on Thursday, May 28 2009 |
Today
a reader asked me if I'd ever heard of the Weyl-Dirac theory. I replied
that I have, and I wrote about it on this site some time ago; I think
it's over in one of my post archives.
Anyway, the theory
really is nothing more than Weyl's action Lagrangian with a
modification made by Paul Dirac in 1973. To me, it's an ugly theory and
one unbecoming the great Dirac, who once remarked that good equations
have to be beautiful.
But the Weyl-Dirac "theory" still pops up
occasionally, the latest being an otherwise excellent overview of the
idea provided by the German Weyl-expert Eric Scholz. (Here's what
appears to be an overhead presentation he gave in February of this year.)
The
article includes a reference to a paper on the theory by Nathan Rosen
(1909 - 1995), the noted Israeli physicist who was once the young
colleague of Einstein. The paper is entitled "Weyl's Geometry and
Physics," which appeared in the journal Foundations of Physics in 1982.
(Yes, this is the paper I alluded to in my previous post.)
Since
I wasn't able to find the paper anywhere, let me just use this occasion
to mention how strangely circular theoretical physics often is.
Rosen
was the co-author with Einstein (along with Boris Podolsky) of their
famous 1935 paper "Can Quantum-Mechanical Description of Physical
Reality Be Considered Complete?" (Yes, the title's grammar seems to be
wrong, but it was Einstein, you see). In an even earlier post I
mentioned how this paper, and the famous "EPR paradox" it presented to
the world, was voted as one of the top five physics papers of all time.

Thanks again, Wikipedia!
It
was also Einstein and Rosen who came up with a mathematically
consistent gravitational metric that describes a Lorentzian wormhole
(or "Einstein-Rosen bridge"). The wormhole, as every kindergarten kid
knows, is a tubular, traversable deformation in spacetime that can be
used to overcome the local speed limit of light; two points in space
(or time!) can thus be connected superluminally, but only if you happen
to own a wormhole.
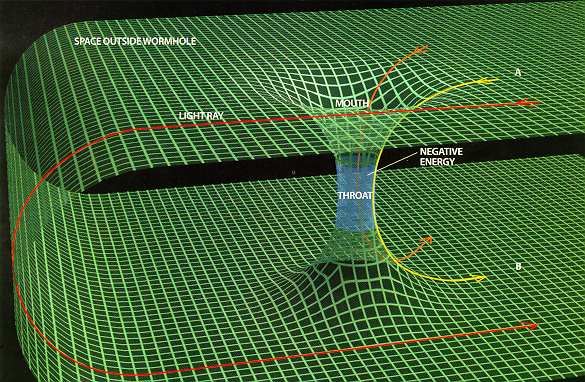
Unfortunately,
in 1962 John Archibald Wheeler (a good buddy of Weyl) proved that
wormholes are unstable and would collapse at the speed of light. Thus,
something is needed to hold the wormhole open long enough for me to get
through (yes, I desperately want to get out of here). It has been
theorized by Kip Thorne and others that such a "Samson-like" substance
might actually exist in the form of some kind of exotic,
negative-energy matter. Alas, Home Depot doesn't carry this stuff yet.
So again we see the familiar tag team of Weyl, Dirac, Einstein and Wheeler, and now we can add Rosen to the list.
If
anyone out there has a copy of Rosen's 1982 Weyl paper, or if you
happen to have a spare non-collapsing wormhole lying around, please let
me know. |
| Some Holes in the Theory -- Posted by wostraub on Saturday, May 23 2009 |
Earlier
I posted the two papers Dirac published in early 1928 on the
relativistic electron. Dirac's electron equation soon became the
cornerstone of modern quantum theory, but it took several years to iron
out its full interpretation. One stumbling block had to do with the
fact that the equation predicted negative energy states for the
electron. Another involved the seeming over-abundance of solutions:
whereas Schrödinger's equation resulted in a single expression for the
electron's wave function, Dirac's gave four — two with positive energy, and two with negative energy.
Paul Adrien Maurice Dirac, 1902 - 1984
It
was soon recognized that the two positive-energy solutions had to do
with the electron's two spin states (up and down), but the
negative-energy states continued to perplex even the brightest
physicists, Dirac included. In his 1929 paper Elektron und Gravitation,
Hermann Weyl proposed that these extra energy solutions might have
something to do with the proton, the only other "elementary" particle
then known (other than the photon). But Weyl subsequently discovered
that the particle associated with these extra solutions had to have the
same mass as the electron. Upon reading Weyl's paper and considering
his ideas, Dirac was motivated to come up with another answer, that of holes in an electron sea.
Dirac's
basic idea was this: an ordinary, free, positive-energy electron was
fully allowed to collapse into a negative energy state, but if all
those states around it were filled it would be prevented from doing so
by the Pauli exclusion principle. Dirac envisioned a universe bathed in
a "sea" of negative-energy "holes," which ordinarily prevented a
garden-variety electron from collapsing into a negative energy state.
But these "holes" also acted like particles having the same mass as an
electron, and they were also allowed to propagate into the overlying
positive-energy sea, though the exclusion principle still held.
Although
Dirac's hole theory was praised at the time as a remarkable achievement
in itself, Dirac was still bothered by its tenuous interpretation. In
May 1931, he published a paper in which the hole theory was abandoned.
In its place, Dirac proposed that the negative-energy states
represented ordinary particles identical to electrons with the
exception that they had positive charges. This bold prediction became the basis for the concept of antimatter.
While Dirac had little to support his idea except for some fancy
mathematics, he intuitively felt it to be correct. Then in 1932 the
Caltech physicist Carl Anderson announced the discovery of the
antielectron, which today is known as the positron. The
positron, along with antiprotons, antineutrons and a veritable zoo of
other forms of antimatter, have all been produced countless times in
high-energy particle experiments and are an indisputable and
inescapable consequence of modern quantum field theory. Dirac is
therefore rightfully called the father of antimatter.
Years
later, the famed Caltech physicist Richard Feynman provided a brilliant
interpretation of antiparticles that is completely consistent with the
mathematics he used to describe them. Noting that the term exp(-iEt/ℏ) invariably accompanies positive-energy particle expressions (where E, t
are the energy and time and ℏ is Planck's constant divided by 2π),
Feynman discovered that the term was invariant when describing
negative-energy antiparticles propagating backward in time.
(I recall a talk show many years ago — it may have been Dick Cavett —
in which Feynman discussed this idea, completely flabbergasting his
host.)
Dirac won the Nobel Prize in Physics in 1933 at the age
of 31. He is inarguably the equal of Isaac Newton as the greatest
physicist who ever lived (Dirac's powers far exceeded those of
Einstein), and it is a great wonder to today's physicists that Dirac's
name is largely unknown to the general public.
Dirac knew
Hermann Weyl well and was often intimidated by Weyl's own prowess,
although he considered Weyl to be primarily a mathematical genius with
a gift for physics. Nevertheless, he admired Weyl's tendency to see
physical truth in mathematics alone, and once admitted that he would
have dismissed his hole theory immediately if he had maintained
absolute faith in the mathematics of his electron equation. Dirac once
wroteWeyl was a mathematician. He was not a physicist at
all. He was just concerned with the mathematical consequences of an
idea, working out what can be deduced from the various symmetries. And
this mathematical approach led directly to the conclusion that the
holes would have to have the same mass as the electrons. Weyl did not
make any comments on the physical assertions. Perhaps he did not really
care what the physical implications were. He was just concerned with
achieving consistent mathematics. Like Weyl, Dirac was quick to give credit to others. You may be interested to know that the famous Heisenberg equation of motion
i ℏ dA/dt = [A, H] + i ℏ ∂A/∂t
which describes the total time dependence of an operator A in terms of its commutation with the Hamiltonian energy operator H, was in fact first derived by Dirac. Dirac ascribed the equation to Heisenberg in his 1930 book Principles of Quantum Mechanics solely out of professional deference to an esteemed colleague that he did not always see eye to eye with! |
| More on Weyl -- Posted by wostraub on Monday, May 4 2009 |
I've been perusing Katherine Brading's 2001 PhD dissertation Symmetries, Conservation Laws and Noether's Theorem, which is available online.
Brading is a professor of philosophy at Notre Dame University in
Indiana and, while I don't really understand philosophy at all, her
mathematical arguments are not only understandable but insightful as
well.
Brading has given the best description of why local
gauge symmetry is not only beautiful but necessary, although the basic
idea has been addressed by many researchers over the years.
Essentially, it's this:
In the action Lagrangians for quantum theories, one always finds terms such as Ψ*Ψ,
either as written here or in combination with their first derivatives
with respect to spacetime. If one replaces Ψ with exp(-iΛ) Ψ (where the
coefficient Λ is a constant), the Lagrangian does not change because
the mulitplier exp(-iΛ) and its complex conjugate cancel one another.
Because the coefficient is a constant everywhere, one therefore says
that quantum physics is invariant with respect to a global
change of gauge. But if we demand that the coefficient be a constant
over all spacetime, it has to be set up simultaneously as one moves
from one point to another. This violates the spirit of special
relativity, which says that a physical effect cannot occur faster than
the speed of light.
Consequently, one has to abandon the idea
of a constant Λ and replace it instead with a coefficient that is
allowed to change continuously from point to point. The multiplier then
becomes exp[-iΛ(x)]. Since this change has to be completely arbitrary
(otherwise it would still violate special relativity), the coefficient
Λ(x) must itself be totally arbitrary and structureless. This gives
maximum freedom to the gauge, and we now have what is called a local gauge symmetry. (In modern quantum theory, the coefficient Λ is proportional to a square matrix, which sets up the action for the strong nuclear force.)
However, derivatives such as ∂μ
exp(-iΛ)Ψ will now bring down derivatives of the gauge multiplier into
the Lagrangian as well and, unless these cancel somehow, the action
will no longer be gauge invariant. We are thus obliged to introduce
additional terms into the Lagrangian that will provide this
cancellation. These terms essentially serve as electrodynamic
interactions, while the terms involving Ψ and its derivatives act as
the kinetic terms. The completed action is now fully gauge invariant,
and its variation with respect to the gauge parameter leads immediately
to the familiar law of conservation of electric charge. The action is
also automatically invariant with regard to position, momentum, angular
momentum, energy and other conserved quantities. Beautiful beyond
belief!

Of
course, Hermann Weyl was not aware of the quantum wave function Ψ when
he developed his first gauge theory in 1918, as quantum mechanics had
not yet been discovered. But his basic idea that nature should be gauge
invariant was essentially correct, and he eventually carried the idea
over into quantum physics in his 1929 foundation paper Elektron und Gravitation. |
| Eighty Years -- Posted by wostraub on Sunday, May 3 2009 |
Eighty years ago this month Hermann Weyl published a seminal paper (Elektron und Gravitation,
Zeit. f. Physik 330 56) that forever changed how we view nature. The
paper introduced numerous new and/or novel applications of mathematical
physics, several of which were vigorously attacked at the time of
publication on the basis of their interpretation within the then
still-evolving quantum theory. While full vindication of these efforts
came about only shortly after his death in 1955, I believe Weyl
witnessed enough progress in modern physics to have been more than
satisfied with his contributions.
Although Weyl had more or less
abandoned his earlier 1918 metric gauge theory (also known as conformal
invariance), by 1929 he was still intrigued by the deep mathematical
symmetries he sensed between gravity and electromagnetism. Weyl also
thought that a true unification of these forces would shed light on the
problem of matter, which was another subject of great interest to him from the previous decade.
The
primary accomplishment of Weyl's 1929 paper was his derivation of the
formal relationship between charge conservation and the gauge (phase)
invariance of the quantum mechanical wave function. But what is so
fascinating about the paper is Weyl's orthogonal approach to the
problem. He first developed a 2-component spinor formalism which
established the basic mathematical physics behind neutrinos, parity
violation and time reversal — ideas that were to stun later physicists
when they realized the full extent of their importance in the 1950s.
Weyl then formalized the use of local tetrads (also known as
vierbeins) as a means of transcribing quantum physics into curved
manifolds, particularly spinors in non-flat space. In doing so, he
discovered the spin connection, a kind of affine connection
for spinor space akin to the ordinary connection term found in
Riemannian geometry. With his tetrad formalism, Weyl then established a
profound similarity between the Riemann curvature tensor R and the electromagnetic field tensor F. Today's physicists still shake their heads in awe at this similarity.
It
was not until the very last section of his paper that Weyl established
the connection between the gauge principle and electrodynamics. It is
here that Weyl took the basic idea of global phase invariance and
brilliantly extended it to the non-local case. Weyl thus established
the abelian U(1) symmetry property of modern quantum mechanics. Weyl's
1929 paper also acted the the impetus for subsequent generalization of
this symmetry to the non-abelian case. It is unfortunate that Weyl (who
died in 1955) appeared to have been unaware of the 1954 Yang-Mills
theory, a seminal paper in it own right which established the
non-abelian approach to the description of the strong nuclear force.
[For a very readable contemporary discussion of these ideas, see Katherine Brading's excellent overview of Weyl's charge conservation principle and Noether's theorem.]
Although
primarily a mathematician, Weyl was one of the earliest to also carry
out fundamental investigations in mathematical physics. He was
therefore a somewhat more enlightened individual than his friend and
colleague Einstein, who was a brilliant physicist but rather plodding
mathematician (the great German mathematician Hilbert once remarked
that any Göttingen schoolboy knew more mathematics than Einstein). The
source of Weyl's fascination in physics was of course his deep
recognition of the profound mathematical symmetries that lie in nature.
Indeed, in 1960 the Nobel physicist Eugene Wigner
wrote a paper expounding on the "unreasonable effectiveness" of
mathematics in the natural sciences. In his paper Wigner addresses the
completely inexplicable success of man's physical theories, not only as
described by mathematics but as a consequence of
mathematics. We now know that mathematical symmetries are largely (if
not solely) responsible for this success, and it is through the action
principle (or variational principle) that these symmetries translate
into all the known physical and conservation laws.
Symmetry is a form of beauty, and beauty speaks for truth. Who but God could have set down these mathematical principles? |
| The Greatest -- Posted by wostraub on Monday, March 23 2009 |
Several years ago Discover magazine asked its readers to name the greatest physics papers of all time. The top five were Newton's Principia
(which was actually a book); Einstein's 1915 general theory of
relativity; the Einstein-Podolsky-Rosen paper of 1935 (see my write-up
on Bell's Inequality for more information); Noether's 1918 paper on
symmetry and conservation laws (see my write-up on Weyl and Higgs
Theory); and Dirac's two-part paper from 1928 on the relativistic
electron equation (see my write-up on Weyl Spinors and the Dirac
Equation).

I don't remember if any single paper actually won top honors, but I voted for Dirac.
In
my opinion, Dirac's electron equation represents the greatest
intellectual achievement of humankind. The paper, published in the Proceedings of the Royal Society
when Dirac was only 25 years and a few months of age, was universally
hailed as a work of highest genius. The equation, and the wonderful
matrices that Dirac discovered, quickly became the cornerstone of all
modern quantum physics.
I've been asked on numerous occasions
to post Dirac's two-part paper on this website, and here it is at last.
My copy of Part I is of rather poor quality, but it's still quite
readable.
Eighty-one years ago, God spoke to Dirac's mind. The Quantum Theory of the Electron is the result of that interaction. Enjoy.
Part 1
Part 2 |