|
|
2006 Archives
| The
Conformal Tensor and Weyl's Gauge Theory -- Posted by
wostraub on Tuesday, December 19
2006 |
Some time ago I wrote
about Weyl’s conformal tensor. It has some neat properties, but it
usually crops up only in a gravitation/cosmology context, and hardly
ever in differential geometry. But it was in that sense that the
conformal tensor was used by Einstein to get around his primary
objection to Weyl’s 1918 gauge theory, which was that the line element
ds is not invariant with respect to a metric gauge
transformation (also known as a conformal transformation of the metric).
Recall that an infinitesimal local gauge transformation of the metric
gμν → (1 + ε π) gμν regauges the lengths
or magnitudes of vectors under physical transport, where π(x)
is the gauge parameter. Consequently, the line element ds2
= gμν dxμdxν is also regauged in
accordance with ds → ½ ε π ds.
Einstein’s argument was that ds can represent time as well as
distance, so time-independent processes such as the spacings of atomic
spectral lines can be invariant only if the line element is gauge
invariant. Since it is not, Einstein thought Weyl’s theory had to be
wrong.
But later, Einstein took up the problem once more. He felt that ds
could be made gauge invariant if the line element were revised to ds2
= J(x) gμν dxμdxν, where J
is a scalar function of the coordinates whose gauge variation goes like
δ J = -ε π J (that is, J must be of gauge weight -1).
This would cancel out the gauge change in the metric tensor and leave
the line element invariant.
Try as he could, Einstein could not come up with an appropriate scalar.
Finally, he noticed that the Weyl conformal tensor Cαμνβ
was exactly what he needed, for the combination √ Cαμνβ Cαμνβ
is of gauge weight -1 in a Riemannian space.
Unfortunately, the Weyl conformal tensor vanishes in the absence of a
gravitational source, leaving a null line element (ds = 0)
whose gauge invariance is now trivial. Furthermore, the counterpart of
the foregoing expression in a Weyl space is unknown.
What Einstein apparently overlooked is the scale factor from the Weyl
theory itself, which considerably simplifies things. Consider the
integral quantity k ∫ φμ dxμ, where k
is a constant and φμ is the Weyl vector (which he
identified as the electromagnetic four-potential). Under a metric gauge
transformation, the Weyl vector varies in accordance with δ φμ
= λ ε ∂μπ, where λ is another constant.
Gauge-transforming the above integral puts the gradient ∂μπ
under the integral, which is easily integrated. We can now set the Weyl
scale factor to J via J = ek ∫ φμ dxμ,
which, by appropriate selection of the constant k, will have
gauge weight -1.
This seems like a better approach than that provided by the conformal
tensor, because in the absence of the electromagnetic potential φμ
the exponential term is identically 1. Thus, the line element can be
made gauge invariant only in a Weyl space containing a non-zero
electromagnetic field!
I haven’t found any evidence that Weyl resorted to this counterargument
to Einstein’s objection, but by that time Weyl had moved on, anyway. In
1929, Weyl applied the gauge concept to quantum theory, which was a huge
success. One has to assume that he never looked back. |
|
Hermann Weyl and Dimensional Reduction -- Posted by
wostraub on Monday, December 18
2006 |
In his neat little
book The Dawning of Gauge Theory, Dublin physicist Lochlainn
O’Raifeartaigh writes
The procedure by which higher-dimensional systems are
reduced to lower-dimensional ones is called dimensional
reduction. The reason that dimensional reduction is so powerful
from the point of view of gauge theory is that it converts
coordinate transformations in the full space into gauge
transformations in the subspace.
Historically, the most famous example of this statement
comes from Kaluza-Klein theory. In 1919, the German physicist Theodor
Kaluza postulated the existence of a fifth dimension which was
hidden from observation because it was too small to be seen. Kaluza
thought that the electromagnetic four-potential of Maxwell’s
electrodynamics resided in this dimension, but that its effects were
observable only in the more familiar four-dimensional world we humans
reside in.
Kaluza assumed that the true metric tensor gμν(x)
was five-dimensional. Viewed as a 5x5 symmetric matrix, it has a 4x4
subblock representing ordinary four-dimensional spacetime, while the
g0μ "boundary" elements include the potential Aμ
by way of the identifications g0μ = g55Aμ
(μ = 0,1,2,3) and g55 is a constant. Thus, the
four-potential Aμ lives in the fifth dimension.
The potential is brought down into our world via dimensional reduction.
Kaluza took as his action quantity the integral
∫ √ –g R d5x
where the metric determinant g and the Ricci scalar R
are the old familiar ones, but now in five-dimensional form. Using
Kaluza’s above formulas for the g0μ quantities, this
five-dimensional integral can be reduced to four-dimensional form, which
is
∫ √ –g (R – FμνFμν ) d4x
This, amazingly, is the familiar expression for the combined
gravitational-electrodynamic action! (Physicist Ian Lawrie considers
this result a minor miracle. It isn't, because God just made it that
way!) I find it remarkable that Kaluza was able to deduce this way back
in 1920, because the calculation (while straightforward) is not trivial.
(Kaluza excitedly sent his paper to Einstein in 1919 to get a
recommendation for publication. Einstein, though quite impressed, was
nevertheless uncomfortable with a five-dimensional world, and so
suppressed publication until 1921. Kaluza was not particularly happy
about this!)
The Swedish physicist Oskar Klein published a subsequent paper in 1926
that made numerous important improvements to Kaluza’s idea in the
context of the then-emerging quantum theory. Hence the theory's present
Kaluza-Klein moniker.
Interestingly, in 1953 the great Austrian physicist Wolfgang Pauli took
Kaluza-Klein theory one step further -- that is, one dimension further,
to n = 6. This resulted in the very first non-abelian approach
to non-gravitational (particle) physics. Several years later, using a
similar approach, Yang and Mills developed the first consistent theory
for the strong interaction.
You might note that, in accordance with O’Raifeartaigh’s assertion, the
coordinate-invariant form of Kaluza’s five-dimensional action results in
a fully gauge-invariant term (√ -g FμνFμν)
following dimensional reduction, while the original action is not gauge
invariant at all. We got a gauge-invariant term by reducing the
dimension by just one; imagine the possibilities if one started with,
say, an eleven-dimensional action! This is the so-called M-theory
of string physics, which promises great things (but has delivered
nothing to date except beautiful mathematics). Note, however, that
Kaluza-Klein theory, while interesting, eventually lapsed into obscurity
because it did not predict any new observable phenomena – it was just a
pretty theory. String theory is now finding itself in the same boat, and
if the legions of brilliant physicists now grinding away (and maybe
wasting their precious talents) at this theory cannot produce anything
predictive from it (like explaining the magnitudes of the gravitational
and electromagnetic coupling constants), it may also be forgotten.
Did Hermann Weyl play around with dimensional reduction? Did he ever
consider the possibilities of a higher-dimensional gauge theory? I’ve
seen no evidence that he ever did. By dying in 1955, Weyl missed
Yang-Mills and a lot of other neat stuff he would have undoubtedly
contributed to.
Weyl was taken from us too soon. |
|
Louise Brooks: Lulu Forever -- Posted by
wostraub on Saturday, December 16
2006 |
Peter Cowie's new book
Louise Brooks:Lulu Forever is out, and at long last.
Finally we have a large-format book with hundreds of rarely-seen photos,
motion-picture production stills and first-person accounts of 1920s
actress-flapper Louise Brooks, who would have turned 100 years old last
month (she passed away in 1985).
I probably would not care so much for this actress if it were not for
the fact that I first saw her signature film Pandora's Box
(filmed in Germany as Die Büchse der Pandora) as an
impressionable young college student in 1970. At the same time, I was
taking an elective course in literature (very odd for a chemistry
major), where I was also reading Vladimir Nabokov's irreducible
masterpiece Lolita for the first time. It was in Chapter 6 of
the novel that I encountered Monique, Professor Humbert's French
girl-whore, the predecessor of one Ms. Dolores Haze. To me, Louise and
Monique were one and the same at the time, and I have forgotten neither
in all these years.

Of course, as a Christian I have mixed feelings about all this now, but
literature is literature, and life itself isn't squeaky clean. Humbert,
Monique and Lulu all paid dearly for their shortcomings (as did Louise
Brooks), and so I will let it go at that.
Cowie's book can be purchased from
Amazon for about $35. If you're interested, you might also
consider buying
Lolita* which, in my humble opinion, is the third
greatest book ever written (right behind Hamlet and the New
Testament). Exceedingly well-written, hilarious, disturbing and
heart-breaking at the same time, it's all the more amazing that it was
written by a Russian who picked up the English language later in life
(much like Joseph Conrad, who also ranks right up there).
* Five points to the person who figures out the identity of
John Ray, Jr. PhD, credited as co-author of the book |
|
Bombs Bursting in Air -- Posted by
wostraub on Tuesday, December 12
2006 |
Several weeks ago, I
was driving through San Raphael near San Francisco and happened to stop
by Autodesk, the company founded by AutoCAD's creator, John Walker.
Coincidentally, Walker's name popped up on an Internet search with that
of John von Neumann, the great
mathematical
physicist and close friend/colleague of Hermann Weyl (see my
December 9 post). Von Neumann worked on the Manhattan Project, where
(among many other things) he discovered that an atomic bomb would be
much more destructive if detonated high above the target area (something
involving shock wave pressures, which I know nothing about).
It turns out that John Walker is also interested in such things, if only
academically (unlike me, he is extremely wealthy and has even more time
on his hands). He has a
website that explains the effects of nuclear weapons on human
populations, something we should all get familiar with as long as
President Bush is running the world.
Anyway, Walker's site includes print-out materials and instructions for
making a nuclear effects calculator. It's basically a circular
slide rule that will allow you to ponder (in a very quantitative way)
the death and destruction that a nuclear device can have on your least
favorite city (Crawford, Texas, for example). Well, I made one, and it's
very neat. It's one way to personally experience the practical aspects
of the complicated science that folks like von Neumann, Oppenheimer and
Teller turned into godless, immoral sin.

[Note: Optimum burst height = maximum resultant death and
destruction]
Walker warns that his calculator won't be of much use in a post-nuclear
war world. But that may not be that far off -- I'll bet you anything
that one of the alternatives Mr. Bush is considering for the New Way
Forward© in Iraq is to nuke Iran, in which case all bets are
off. |
|
Weyl and von Neumann -- Posted by
wostraub on Saturday, December 9 2006 |
From the recollections
of mathematician Herman Goldstine, friend of Hermann Weyl and the great
mathematical physicist John von Neumann, and (with von Neumann) one of
the developers of the early ENIAC computer:

Hermann Heine Goldstine, 1913-2004
"I always was struck by the difference between Weyl
and Johnny von Neumann. There are jokes, one of which Johnny always
swore was false. That's the story that, I don't know, Hermann Weyl
was going to prove some theorem, a very deep and profound theorem,
let's say it was the Riemann-Roch theorem. I don't know if it was
the Reimann-Roch theorem, but that was one I always have trouble
with, so let's say that was the theorem. And Weyl gave a lecture on
why this is a very deep, profound result, and he gave a very
complicated proof. And the apocryphal story goes that at the end of
the lecture there's this kid who is supposed to have raised his hand
at the back of the class and said, 'Professor Weyl, may I show you a
proof?' And goes up to the board and goes zip, zip, zip, zip, and in
about 15 lines has a brilliant proof of this thing.
"I asked Johnny about it, and he said no, that wasn't true. But it
is true, if you talk to Natasha Brunswick, who was in those days
Natasha Artin. Natasha says that there was always Johnny with these
tight pants on. All of Johnny's life, whatever size suit he bought,
he always ate too much, and the suit was always one size smaller
than Johnny. Even as a student in Göttingen, his behind was always
ready to bulge out of his pants. I guess Natasha and everybody in
the class were always charmed.
"But Joachim, who was one of Hermann's children, told me that when
Hermann used to work in his house on Mercer Street, in the study in
there, you would hear groans coming out of the study. That Weyl
worked at things in sort of anguish, that it was hard for him, that
he delivered his theorems practically like a woman giving birth to a
child. That's so different from Johnny, because when he and I would
be working at something, when we'd get stuck, he'd say, 'Okay,
that's it, ' and pack it up. It might be that he'd phone at two in
the morning to say, 'This is how the proof goes.' But it might be
three weeks, a month or so later, or it might even be I who would
come in a month or so later and say, 'This is, maybe, how to go.'
But he never struggled with something. When he got stuck, he filed
it somehow, and it just came out easily. I suspect that Weyl was
probably the deeper of the two mathematicians."
|
|
Louise Brooks at 100 -- Posted by
wostraub on Sunday, December 3 2006 |
[Follow-up to my
October 17 post.] While visiting San Francisco recently, I stopped by
the city's Main Public Library, which is featuring an exhibit on the
American actress Louise Brooks. Brooks, who passed away in 1985, would
have turned 100 on November 14.

Astonishingly beautiful, Brooks created the movies' "bobbed" hairstyle
look around 1926. I still remember the recollections of my late mother
who, as a lovely teenager herself in the late 1920s, begged and begged
her parents to get her hair bobbed á la Brooks. But as strict
Southern Baptists, such a hairstyle (not to mention even going to the
movies!) was absolutely verboten.
Back from SF, I was happy to have finally received
Criterion Collection's two-disc DVD set of Brooks' early 1929
psycho-sexual drama Pandora's Box, the actress' signature film
(filmed in Berlin by the great German director, Georg Wilhem Pabst).
Regarded as one of the top ten greatest silent movies of all time,
Criterion's digitally remastered version of the Munich Museum's restored
film includes four different musical scores, Lulu in Berlin (a
rare filmed interview with the actress, produced in 1984), Looking
for Lulu (the one-hour, 1998 Hugh Neeley documentary on Brooks'
life), the book Reflections on Pandora's Box, and assorted
essays, audio commentaries, interviews and stills. If you're into this
actress, this is a must-have DVD.

Brooks at age 64, in a rare 1971 interview with British filmmaker/
film essayist (and Harvard physics graduate!) Richard Leacock
Tragically, parental neglect and childhood sexual abuse (at the age of
nine) most likely destroyed Brooks' life, and she went on to become the
same kind of woman she portrayed in Pandora's Box and Diary
of a Lost Girl (also 1929). An ultra-liberal, chain-smoking,
alcoholic, partying sexual abandonee and iconoclastic loner until very
late in life, to her enduring credit she renewed her Catholic roots,
took up writing and turned herself around. She died of emphysema at the
age of 78. May God save her soul.
My candle burns at both ends;
It will not last the night;
But ah, my foes, and oh, my friends--
It gives a lovely light! -- Edna St.
Vincent Millay (1920)
[More pics of the exhibit can be found
here] |
|
Another Hermann -- Posted by
wostraub on Monday, November 27 2006 |
If you’ve read my
articles on Weyl spinors, Dirac’s equation and quantum field theory (or
been bored by them), then you’ve probably wondered why no mention was
made of Grassmann numbers.
In QFT, scalar particles and fields can be described by a path integral
involving infinite-dimensional products (dφ1dφ2dφ3…dφinfinity
) under the integrals. But for fermions (electrons, quarks and the
like), whose fields are actually operators, the fields ψ(x)
obey instead an anticommuting algebra. Thus, ψ1ψ2
= - ψ2ψ1, which needless to say complicates
fermionic QFT. The first thing I thought when I saw this was “well,
matrices and differential operators can anticommute, so these fields are
just matrices or differentials.” No, I was wrong -- there are plain old
ordinary numbers out there that can anticommute. They are called
Grassmann numbers.
Hermann Grassmann was born in Stettin, Germany in 1809. He loved math
and physics, but was also drawn to theology, chemistry, Latin,
philosophy, linguistics and neohumanism, so much so that he ultimately
went on to teach all of these subjects. Amazingly, he never took any
formal classes in mathematics or physics, yet he excelled in these
subjects to the extent that famous mathematicians of the day (including
Möbius and Kummer) considered him their equal. But because he was not
formally educated, Grassmann was not recognized in his day for his
genius.

Grassmann was apparently the first researcher to realize that linear
vector spaces need not be limited to three dimensions. His work on
infinite-dimensional vector spaces predated by many years the work of
Hermann Weyl, Elie Cartan and other mathematicians, but intriguingly it
also provided the mathematical basis for fermionic QFT.
When Einstein tackled gravity in 1911, he found he needed a type of
mathematics that described gravitational physics that did not depend on
any particular coordinate system. He was advised by friends to study
tensor calculus, which had been worked out fifty years earlier by
the likes of Riemann, Christoffel and Ricci. I find it remarkable that
quantum electrodynamics would similarly be worked out in the 1940s using
a mathematics that had been discovered by Grassmann almost one hundred
years earlier.
The books I have on QFT explain only the merest fundamentals of
Grassmann algebra, while math books I have seen on the subject go far
over my head. Still, I am amazed that God could come up with something
so strange and counterintuitive -- and useful. In fact, since fermions
make up all of the ordinary matter in the universe (including you and
me), God must have had Grassmann numbers in mind from the very
beginning. What a Creator!
One of the oddest things about Grassmann calculus is its underlying
simplicity. For example, the most complicated single-variable math
formula f(x) you can think of can be expanded as a Taylor
series, which in Grassmann algebra consists of just two terms: a +
bx, where a and b are constants. Thus, the basics
of Grassmann's discovery can be grasped by anyone in about five minutes.
You can read more about Hermann Grassmann here:
Wikipedia |
|
Units -- Posted by wostraub
on Thursday, November 16 2006 |
One of the more
appealing aspects of Hermann Weyl's metrical gauge theory deals with the
concept of "units." Humans measure length in terms of meters and feet
and, in ancient times, cubits -- different, but all interchangeable, and
therefore the same thing. But in the presence of a strong gravitational
field (or when dealing with velocities approaching the speed of light),
the lengths of physical objects can become ambiguous -- the length of a
physical measuring rod, for example, can depend on the observer.
In Weyl's original gauge theory, length can be continuously redefined as
one goes from one point in spacetime to another.
The basic units of length, time, mass etc. used to be based upon
physical objects or anthropological effects (all called "artifacts")
that were explicitly defined to represent the units they stood
for. For example, the meter used to be defined as 1/10,000,000 of the
distance from the equator to the North Pole (via Paris). Similarly, the
second was once defined as 1/86,400th of a day. In these examples, the
physical earth was a measurement artifact.
All of these artifact-based units (except the unit for mass) have since
been replaced by non-anthropological representations. For example, the
meter is now defined by a specified number of wavelengths of the
emission spectrum of a certain cesium isotope. Similarly, the speed of
light in vacuo is now fixed at exactly 299,729,458 meters per
second. The second itself has a specific definition based on isotopic
transitions. But to date the kilogram has resisted all such conversions.
Officially, it is still defined as the mass of this platinum-iridium
alloy cylinder having equal dimensions of length and diameter (39 mm)
maintained near Paris:

But this object is not entirely stable. It has been observed to change
on the order of 50 parts per billion per year (Corrosion? Sublimation?
Old age?). Now scientists are attempting to revise the definition of a
kilogram to a non-artifact basis. But it has been a difficult road.
The December issue of Scientific American describes the most
recent attempt. It is based on a nearly perfect, ultra-pure sphere of
crystalline silicon-28 having a number of atoms that is very nearly that
of Avogadro's number (roughly 6 x 1023), which is defined
itself as the number of anything in one mole of a pure elemental
substance.
But to my mind, this just replaces one artifact with another.
Furthermore, Avogadro's number is another "unit" having an
anthropological basis. Is there no way to define the unit of mass that
is free of some kind of human subjectivity?
Quantum physicists long ago realized that their equations could be
greatly simplified by setting Planck's constant and the speed of light
to unity. But this is really nothing more than a convenience, as these
simplifications only establish yet another set of units that is no
better than any other now in use.
My suggestion? Define the kilogram as the mass of one atom of hydrogen
and be done with it. |
|
Weyl and Einstein, Again -- Posted by
wostraub on Friday, November 10
2006 |
Taken aback by Hermann
Weyl's insistence that his gauge theory was valid despite the physical
evidence, Einstein wrote to his friend on 1 May 1918 with this
remarkable correspondence:
Could one really charge the Lord with inconsequence
for not seizing the opportunity you have found to harmonize the
physical world? I think not. If He had made the world
according to you, you see, Weyl II would have come along to address
Him reproachfully thus:
"Dear Lord, if it did not suit Thy way to give objective meaning to
the congruency of infinitesimal rigid bodies, so that when they are
at a distance from one another one cannot know whether or not they
were congruent, then why didst Thou, Inscrutable One, not decline to
leave this property to the angle or to the similarity? If two
infinitely small, initially congruent bodies K, K' are no
longer able to be brought into congruency after K' has
made a round trip through space, why should the similarity
between K and K' remain intact during this round trip? So
it does not seem more natural for the transformation of K'
relative to K to be more general than affine."
But because the Lord had already noticed, long before the
development of theoretical physics, that He cannot do justice to the
opinions of mankind, He simply does as He sees fit.
You may not always agree with Einstein, but he just nails
it here. |
|
Stupid Notation -- Posted by
wostraub on Friday, November 10 2006 |
From September 1918
until late November of that year, Hermann Weyl and Einstein corresponded
repeatedly, with the main topic being Weyl's geometrical gauge theory.
Einstein loved the basic idea, but was upset over the fact that the line
element
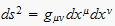
in the theory was not gauge invariant. This unsettling little fact
ultimately doomed Weyl's idea.
But the two also bickered over Weyl's expression for the equation of the
geodesics, which is obtained by extremalizing the related integral
expression
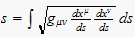 . .
Weyl's result was
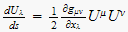
where
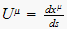
Einstein vehemently stated that this was wrong. Weyl disagreed, and for
three months the issue came up again and again. The two men never
resolved it, and Weyl persisted in using his expression in all five
editions of his book Space-Time-matter. So who was correct?
Well, Einstein was right after all, but the whole thing was trivial, and
the two great scientists should have known better. The correct
expression is
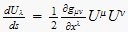
What's the difference? It's in the partial derivative term for the
metric tensor: Weyl used a covariant term for x in the
denominator when he should have used the contravariant term.
It's no big deal, but it serves to show how important it is to maintain
consistency in your tensor notation. Few areas of mathematics have
displayed such a wide and bewildering range of notation as has tensor
calculus in its 150-year history. In the years immediately following
Einstein's general relativity theory, it seems that everyone was using a
different notation (even Einstein). Contravariant and covariant indices
were constantly being intermixed, and that is really what lies at the
bottom of this little Weyl-Einstein disagreement. |
|
Spin and the Early Universe -- Posted by
wostraub on Thursday, October 19
2006 |
Abraham Loeb,
Professor of Astronomy at Harvard University, has an interesting article
in the November issue of Scientific American that deals with
the so-called "Dark Ages" of the universe.
According to current cosmological thought, about 380,000 years after the
Big Bang the universe had cooled enough for neutral (non-ionized)
hydrogen atoms to form. This prevented the microwave background
radiation from continuing to interact with electrons and ionized
hydrogen via Thomson scattering, so it began to leak out into the
expanding universe. Because stars had not yet started to form, there was
no source of light, and the universe went almost completely dark -- the
start of the Dark Ages.
During this darkness, which is believed to have lasted about a billion
years, gravitation gradually coalesced matter into stars and galaxies.
Light radiation from the resulting fusion reactions reionized most of
the hydrogen in the still-expanding universe, and light returned to the
cosmos.
As a consequence, the farthest astronomers can see with their telescopes
is about one billion light years. Whatever occurred prior to that cannot
be detected.
Or can it? Loeb believes that the universe preserves an imprint of the
Dark Ages through what he calls a menage a trois between the backround
radiation, the kinetic energy of neutral atoms, and a type of energy
called hydrogen spin energy. By modeling how these energies must have
interacted, astronomers can compare theoretical calculations with
observations of the sky at long radio wavelengths and test it out.
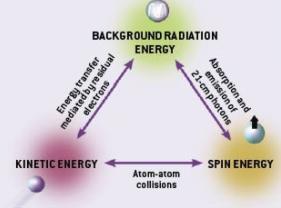
In the article, Loeb describes how a neutral hydrogen atom, consisting
of a proton and electron, can exist in its ground state in two distinct
energy states -- one with the spins of the proton and electron aligned,
and another in which the spins oppose each other. The energy difference
is minute, but becomes important when the background radiation level or
kinetic energy is smaller. Loeb believes that as the dark universe
expanded, the spin energy, radiation energy and kinetic energy took
turns being top dog, and that the echoes of this cosmic energy dance are
still detectable in the night sky.
If Loeb is right, then humans will be able to see the unseen, and
perhaps get an even better glimpse of the hand and mind of God.
|
|
Pandora's Box on IFC -- Posted by
wostraub on Tuesday, October 17
2006 |
Shot in Berlin in the
waning years of Germany's Weimar Republic, the late silent film classic,
"Pandora's Box" (Die Büchse der Pandora) is airing on the
Independent Film Channel (IFC) at midnight tonight and tomorrow at 7:45
am PST (October 18). The film is shown uncut and uninterrupted, with
both its original German and English subtitles.

German filmmaker Georg Wilhelm Pabst's 1929 classic stars the hauntingly
beautiful American actress Louise Brooks (1906-85) as the libertine but
curiously innocent dancer/vamp Lulu. Now widely regarded as a cinematic
masterpiece, the film received surprisingly scathing reviews because of
its (then) shocking sexuality (but there's no nudity, parents).
Sickened by the excess and amorality of Hollywood (though hardly an
ingenue herself), and stuck in a series of profitable but brainless
"flapper" roles, Louise Brooks left to further her career in Germany,
where she starred as Lulu in "Pandora" and Thymiane in "Diary of a Lost
Girl" (Das Tagebuch einer Verlorenen, also 1929). Following
another starring role in the 1930 French film Prix de Beauté
("Beauty Prize"), Brooks returned to the states. She grudgingly made
several more films in the 1930s, but she was essentially blacklisted by
the film industry because she refused to play by its rules. She left
Hollywood for good in 1939 and went to New York, where she lived a
rather impoverished, hand-to-mouth existence as best she could until her
death in 1985.
A victim of childhood sexual abuse and gross parental neglect, Brooks
ironically and tragically became a hedonistic abandonee herself, and by
the mid 1950s was, in her own words, "a questionable East Side dame."
But about that time she started writing about her life and the many
stars she had known personally (often very personally) during
her acting days. While her work was not prolific, her writing
demonstrates a remarkable talent for intelligent exposition. Her 1982
book, Lulu in Hollywood, reflects a truly brilliant mind.
A chronic drinker and smoker, Brooks succumbed to emphysema on August 8,
1985 after a long struggle with the disease.
Brooks led an absolutely amazing life, which is chronicled in Barry
Paris' excellent 1989 book, Louise Brooks: A Biography.
Silent film fans around the world will celebrate Louise's 100th birthday
next month (on November 14), at which time Criterion Collection Films
will release a digitally remastered DVD of Pandora with many extras,
including a rare filmed interview of the actress from 1979. |
|
Melvin Schwartz Dead at 73 -- Posted by
wostraub on Wednesday, August 30
2006 |
1988 Nobel Prize
winner Melvin Schwartz has died at 73. He shared the prize with Leon
Lederman (The God Particle) and Jack Steinberger for their work
on the weak interaction and their discovery that neutrinos come in
different flavors. But what appealed most to me about Schwartz was his
approach to electromagnetism.
Like many other befuddled graduate students in the 1970s, I had the
great misfortune of being forced to learn electrodynamics from J.
Jackson's Classical Electrodynamics, arguably the most
difficult text on the subject (the third edition was presumably "dumbed
down" in the 1990s in belated response). It's a shame that Schwartz'
Principles of Electrodynamics, first published in 1972, didn't
achieve the same (inexplicable) popularity as Jackson's book, because
Schwartz' approach is much clearer. It's even entertaining -- he starts
it off with the statement Electrodynamic theory is beautiful!
What a wonderful way to start a book!
Schwartz was one of the few physicists who insisted that electric and
magnetic fields, which are essentially the same thing, share the same
units. This in itself represents a tremendous simplication of the
subject, as the "units problem" in electrodynamics has caused no end of
troubles for students.
He similarly simplifies the understanding and calculation of the
Lienard-Wiechert potentials, another chronic stumbling block for
mediocre students like myself. The subject is laid bare in a wonderful
chapter entitled Let There Be Light!, in which the author
unashamedly shares his enthusiam for and appreciation of God's
scientific and mathematical wisdom. Indeed, Schwartz' writing style is
peppered with statements like At this point when the laws were being
written, God had to make a decision ... God naturally chose the
antisymmetric tensor as His medium of expression (Chapter 3). I
love it!
Fortunately, Schwartz' book is available as a
Dover reprint and can be had for about $10, so you have no
excuse for not buying it. No physics library should be without it.
|
|
Dark Matter Discovered? -- Posted by
wostraub on Tuesday, August 22
2006 |
On August 15, a group
of astrophysicists announced they had seen indirect evidence for the
existence of dark matter. What does this mean?
For decades, astronomers have noticed that the rate of rotation of
galaxies does not jive with the amount of matter contained in them –
that is, there is not enough gravity contained in the galaxies to keep
them from flying apart. Astronomers therefore believe that there must be
a form of matter unlike normal matter that keeps the galaxies together.
This matter have been given the name dark matter. It is
optically invisible because it does not interact with ordinary matter.

Scientists have no idea what dark matter is composed of. Since it cannot
be made of ordinary stuff like protons and electrons, other, more exotic
forms of matter have been proposed (axions, anyons, etc.). But to date,
all this conjecturing has been purely theoretical.
Now a team of scientists (including members from the Stanford Linear
Accelerator Center and the University of Arizona) have announced
indirect evidence of dark matter in the Bullet Cluster, two
groups of over one thousand small galaxies that collided about 100
million years ago in the constellation Carina, forming the shock wave
shown in the above photo (which is a composite of visible and x-ray
photographs). As the galaxies collided, the ordinary matter slowed down
as one would expect in any physical collision. However, the dark matter
component, which is immune to any kind of physical (mainly
electromagnetic) interaction, kept right on going. The scientists were
able to deduce this by measuring the amount of gravitational lensing
caused by the dark matter on more distant galaxies seen in the photo's
background (dark matter may not interact directly with ordinary matter,
but it can still affect it gravitationally). Thus, a cosmic collision
event can serve as a means of "filtering out" dark matter from its
ordinary counterpart. Indeed, there is speculation that past events have
generated "dark matter galaxies," whose presence can only be deduced by
gravitational lensing effects.
[Interesting Question: Is intelligent dark matter "life" possible, or
does it require the usual quarks and leptons? Maybe God is not quarkic/leptonic
at all!]
Who cares, you might be tempted to say. But astrophysicists have
estimated that dark matter makes up about 25% of the total matter in the
universe, whereas ordinary matter accounts for only about 5%. The
remaining 70% is thought to consist of dark energy, a
hypothetical energy field (called quintessence by some
scientists) that permeates the entire universe. Thus, the visible
universe you and I know and love accounts for only 5% of physical
reality. This concept is truly mind-boggling.
Hermann Weyl and others postulated that what we today call dark energy
is nothing more than a mathematical artifact of Einstein’s general
theory of relativity called the cosmological constant (I tend
to agree, as "quintessence" sounds a tad like the old "ether" idea of
the early 1900s). The cosmological constant is simply a term in
Einstein’s gravitational field equations which, depending on its sign,
can either act with or against the usual attractive force of gravity.
Many scientists believe that a non-zero, repulsive cosmological constant
exists and is responsible for the observed large-scale repulsion effect
that is forcing the universe to expand at ever-greater velocities. If
true, the universe will eventually expand at the speed of light,
resulting in a rather bleak future for all existence.
The relationship between dark matter and dark energy has not been
established. If the human race can keep from blowing itself up over
petty tribal conflicts (which I find highly doubtful), we may have a
chance at someday understanding the fantastic universe that God has made
for us. |
|
String Theory Unraveling? -- Posted by
wostraub on Tuesday, August 15
2006 |
The great Austrian
physicist Wolfgang Pauli once remarked "What God hath put asunder, let
no man join." He was referring to the seemingly-intractable problem of
unifying quantum theory with general relativity, two theories that work
just fine by themselves but which have, since Hermann Weyl's time,
resisted all attempts at unification. It's the one great open problem of
physics, and every physicist worth his salt worries about it.
Why bother with unification when the theories work fine on their own?
Because only through unification can we simplify our world and begin to
grasp the mind of God. Recall James Clerk Maxwell, who in the 1860s
discovered that the electric field and magnetic field are the exact same
thing. Instead of a hodgepodge of unconnected, complicated vector
equations, we have the four Maxwell equations expressing the unified
electromagnetic field (which, I might add, are among the most beautiful
mathematical expressions mankind has ever gotten its hands on).
The unification problem can be traced to the fact that the general
theory of relativity is not renormalizable (which means that infinite
probabilities invariably arise during the perturbation step), so efforts
to describe gravitation using a quantum-perturbative approach fail
miserably.
Thirty-odd years ago, string theory promised a way around this problem.
The theory's early developers noted that it demands the existence of a
massive, spin-two particle, and it was assumed that the as-yet
undetected graviton feld would fit the bill.
Initially, it looked good on paper. But the most advanced version of
string theory requires that spacetime consist of 11 dimensions (1 time
dimension and 10 spacial dimensions) and not the usual 4. In order to
demonstrate the existence of all these extra dimensions, physicists
would need access to energies that are many magnitudes beyond those
currently produced in the most powerful particle accelerators. Indeed,
these energies rival that of the Big Bang itself, making it almost a
certainty that string theory can never be tested.
The theory's critics insist that any untestable theory is unscientific,
and therefore has no place in science. Some have even gone so far as to
say that it is akin to religious faith. Anti-evolutionists (and
Republicans) might be crazy about this, but not physicists.
My personal problem with string theory is far simpler -- I just can't
follow the mathematics. Back when Einstein first announced his general
theory of relativity in November 1915, it was said that only a dozen
people in the world could understand it. That was simply not true --
relativity is pretty straightforward, and while the math at the time was
unfamiliar, it wasn't difficult at all. Same thing with Heisenberg's
matrix mechanics in 1925 -- physicists just weren't all that familiar
with matrices, which even today's middle school kids can understand.
String theory, by comparison, is nothing less than a convoluted maze of
unbelievably complicated mathematics that seems beautiful only to the
relatively few people who can work with it. And in their own words, even
they don't really understand what they're doing!
So now we get the August 21 issue of Time magazine, which has
an article entitled The Unraveling of String Theory. It reports
that two new books by respectable physicists (Lee Smolin and Peter Woit)
are heralding a renewed criticism of string theory that might just catch
on.
The criticism advances the now decades-long suspicion that string
theory, which provides absolutely no testable predictions, may be
nothing but mathematics after all. If this can somehow be demonstrated,
it would serve to free up the minds of some pretty smart people (like Ed
Witten at the Institute for Advanced Study at Princeton) who currently
are obsessively pursuing M-theory, which is the 11-dimensional version
of strings I mentioned earlier.
In my mind, it's entirely possible that God considered basing physical
reality on string theory, but gave it up because it gave even him
headaches -- and a theory with headaches lacks beauty, and God's way of
thinking always involves beauty. But if not strings, then what? Is there
no way to unify gravity with quantum mechanics? Was Pauli's admonition
correct after all?
If string theory bombs, then we're back to where Weyl, Einstein, Pauli
and many others were 80 and 90 years ago. To be sure, we know a lot more
than those folks did, but one thing remains the same -- our intellectual
curiosity is simply not matched by our intellectual ability.
|
|
Straumann Again -- Posted by
wostraub on Thursday, August 3 2006 |
Here's a new article
from Norbert Straumann (University of Zürich), which was the basis of a
talk he gave in 2005. Some new stuff on Hermann Weyl and early gauge
theory, along with some reflections on the gauge principle in quantum
electrodynamics.
Article |
|
Persistence -- Posted by wostraub
on Monday, July 31 2006 |
Edison once said that
discovery is 1% inspiration and 99% perspiration. Einstein asserted that
persistence trumps intelligence. Weyl's efforts to bail out his 1918
metrical gauge theory certainly represents a classic example of
persistence in the face of withering criticism. Weyl persisted because
he believed he was in possession of the truth.
Recall that Mr Einstein rejected Hermann Weyl’s original gauge theory on
the basis that it did not preserve the invariance of the line element
ds under a gauge transformation. In spite of the simplicity of
Einstein’s argument, Weyl tied himself in knots desperately looking for
a way out. As far as I know, he tried three escape routes.
One was to assume that the ds of measurement was not the same
as the mathematical ds. That is, what we measure as ds
is a true invariant, whereas the mathematical version is not. This
almost metaphysical option was quickly dismissed by Einstein, Pauli,
Eddington and others.
Weyl then moved on to a line element that replaced the metric tensor
gμν with the Ricci tensor Rμν, a
quantity that is a true gauge invariant in Weyl’s geometry. This was an
interesting dodge, but it too was thrown out.
Weyl’s last gasp was to make ds invariant by multiplying the
metric tensor with a scalar J(x) of gauge weight –1, so that
the line element now goes like ds2 = J gμν dxμdxν.
After considerable thought, Weyl realized that the only reasonable J-quantity
had to be the square root of Cμναβ Cμναβ,
where the C-quantity is the Weyl conformal tensor (see my pdf
article on this tensor on the menu to the left). This time Einstein was
impressed, though to this day no one knows if Weyl’s J-quantity
has any relevance in physics.
It is straightforward, if rather tedious, to calculate the equations of
the geodesics associated with Weyl’s J-invariant. I did the
calculation many years ago, and found that they’re completely
nonsensical. I’m sure Weyl did the same calculation, and maybe that’s
when he finally tossed in the towel. |
|
Riemannian Vectors in a Weyl Space -- Posted by
wostraub on Sunday, July 16 2006 |
I've posted the final
write-up on Riemannian Vectors in a Weyl Space, which tries to
address a mathematical inconsistency in the original Weyl theory (and
which has nothing to do with the conformal aspects of the theory).
Fixing the inconsistency leads to simple derivations of the Klein-Gordon
and Dirac equations. I've also included lots of other junk as food for
thought.
In this paper I've tried to include all the reasons why I think Weyl was
really close to a unified theory of the combined gravitational-electrodynamic
field, but please believe me when I say I have no illusions that this
will ever be rigorously demonstrated -- certainly not by my
overly-simplistic treatment. Feel free to criticize.
Riemannian Vectors in a
Weyl Space |
|
Houston, We Have a Problem -- Posted by
wostraub on Saturday, July 15
2006 |
The disturbing events
in the Middle East and the recent hoopla over the space shuttle mission
made me think about that old science fiction movie in which astronauts
take off for the moon or Mars or someplace only to learn that a world
war has destroyed earth's population (along with everything else) and
they have nothing to return to. I'm also reminded of the scene in
Planet of the Apes (the 1960s version, that is) in which one of the
returning astronauts plants a little American flag in the lifeless soil,
while Charleton Heston laughs hysterically.
Now that the shuttle missions have been reduced to meaningless
public-relations trips designed to see whether the ship's insulation is
still intact, I am again forced to unveil the true stupidity behind
America's "space travel" experience. Here it is:
1. The shuttle orbits at an altitude of about 210 miles. At that height,
the force of gravity is still more than 90% of what it is here on
earth's surface. It's just like an astronautic flea who "soars" above
the surface of an onion by jumping onto the nearest outer skin layer.
The astronauts are not in "outer space."
2. The weightlessness of the astronauts is induced solely by the orbital
centripetal force. If they increased the shuttle's speed by only 2.5%,
they could orbit the earth at a height of one foot.
3. Shuttle missions are incredibly boring. There's little for the
astronauts to do other than maintain their life-support equipment. All
meaningful on-board experiments have been done to death, including
observing how crystals grow and ants propagate in microgravity. In their
free time, the astronauts can look out and see the curvature of the
earth. That's about it.
4. Without the protection of earth's atmosphere, dangerous levels of
cosmic rays constantly permeate the shuttle and its inhabitants. Do you
recall the "flashes of light" reported by Armstrong, Aldrin and Collins
during their interplanetary trip on Apollo 11? Those flashes were caused
by "Z particles" (cosmic ions with atomic weight around that of carbon)
piercing the astronauts' corneas. Meanwhile, microgravity induces rapid
loss of bone density and muscle tone.
5. There are literally thousands of pieces of space junk now orbiting
the earth, from grain-size ejecta particles to car-sized failed
satellites. And it's all flying around at many thousands of miles per
hour -- many times faster than a speeding bullet. NASA mission planners
have to keep track of every known chunk to avoid a catastrophic
collision with the shuttle. One of these days they'll lose track of
something, with disastrous results. All it takes is a particle the size
of a grain of salt.
6. In spite of all the high-tech you see in the orbiter, its boosters
and the tracking equipment, the shuttle is really nothing more than a
fancy Chinese rocket utilizing 2,000-year-old chemical technology.
Chlorine- and nitrogen-containing pollutants spewed out from each launch
measurably impact the earth's biosphere (chlorine is about the worst
thing you can imagine for the ozone layer).
7. President Bush says we're going to Mars! The round trip will take
years, cost more than $100 billion, and if cosmic rays don't kill the
astronauts the boredom will drive them insane. But it's a trip Americans
may have to buy into whether they like it or not, as it's rumored that
Mars has weapons of mass destruction. We can't just stand here and wait
to be killed! They don't call it the Red Planet for nothing!
The real reason why Americans support the "space" program is that they
don't know a solar system from a galaxy, a mile from a megaparsec. I
constantly hear people say things like "Our brave astronauts are out
there among the stars and galaxies, blazing the trail to discovery." No,
they're 200 miles above your head, idiot. And if I ever hear that poem
again about "touching the face of God" (in a nuclear-armed fighter jet,
yet), I'll scream. And "spin-offs"? Please, did we have to spend a
trillion bucks for Tang and freeze-dried ice cream?
All this nonsense, and for what? A trifling trillion dollars or so to
date, and counting! The real purpose of these missions today? That's a
national secret, but I can tell you that it involves looking down on you
and me and everyone else, and not looking out on this wonderful universe
God made for us.
My suggestion? Let's first get our planet in order, make our resources
and human, animal and plant life sustainable, find a way to deal with
our aggressions, then reach for the heavens. Wouldn't this please God
more than what we're doing now? |
|
Weyl and Dirac -- Posted by
wostraub on Monday, June 26 2006 |
Someone asked me for a
copy of a 1973 paper by P.A.M. Dirac today. I got it out of the garage
to email, and read it again for the first time in years. In it, Dirac
uses Weyl's gauge theory in an attempt to explain why the gravitational
constant G should be decreasing with time. In the paper, Dirac
reveals a fondness (if that's the right word) for Weyl that I had missed
earlier. He even provides a counter-argument for Einstein's famous
objection against Weyl's theory.
But then he goes on to describe how a non-moving charged particle in a
Weyl field can be used to break charge symmetry while maintaining CPT
symmetry. Dirac's argument is simple: a vector associated with a
particle in a Weyl field changes magnitude according to dL = φμ
L dxμ. If the particle is at rest, vector length still
changes with the flow of time according to dL = φ0 L dx0,
where φ0 is the Coulomb potential and dx0
= cdt. If the change in length is positive with increasing time,
then it must shrink with decreasing time (and vice versa). Regardless of
the convention you choose, the change in length is effected by the sign
of the particle's charge. Thus, symmetry is broken between positive and
negative charge. It's so beautiful.
Dirac, who won the 1933 Nobel Prize in Physics at the age of 31, was
once asked if there was anyone who was so smart even he couldn't
understand. "Weyl" was Dirac's answer. |
|
Hermann Weyl Resources Online -- Posted by
wostraub on Sunday, June 25 2006 |
Among the papers,
books and articles I have collected on Hermann Weyl are a number of
contributions made by the German mathematical historian Erhard Scholz of
the University of Wupperthal. Scholz has written extensively about
Weyl's mathematics (from a primarily historical perspective), although I
find his English difficult to follow for some reason. Nevertheless, his
online materials are well worth acquiring. Just Google "erhard scholz,
weyl" and you'll finds lots of stuff, mostly in pdf format.
You might also want to Google "john l. bell, weyl" (presumably no
relation to the John S. Bell of Bell's Theorem fame) regarding several
online papers he's written on Weyl and his philosophical leanings. I
really don't "get" philosophy, but it's worth checking out.
Another resource that I have not yet acquired is "Hermann Weyl --
Mathematics and Physics, 1900-1927," a 1991 Harvard University PhD
dissertation by Skuli Sigurdsson. I haven't found it on any of the
online dissertation libraries, so it's probably not out there. I suppose
I'll have to get it directly from Harvard for much more than I care to
pay. I'll let you know if I find it.
[God bless the Pasadena, California Library! It acquired a set of
Einstein's collected writings (German and English translations) after a
loan request I made several months ago. The collection includes many
references to Weyl and his gauge theory and is just plain fun to read.]
|
|
Albert, Mileva and the Noble Engineering Profession -- Posted by
wostraub on Thursday, June 22
2006 |
I've been reading the
letters that Einstein and his first wife, Mileva, wrote to each other in
the period 1914-19. This was a period of increasing estrangement between
the two of them following their split-up around 1913, and the
correspondence ranges from cordial to angry.
The letters take on a decidedly monetary tone after 1916, when it became
apparent that Einstein would eventually win the Nobel Prize. Mileva was
constantly asking for money, and Einstein provided it, often grudgingly.
Indeed, the letters from 1916 to 1919 seem to be nothing but arguments
over money. But Mileva was hard up, unemployed, and looking after two
young children, while Einstein, not yet famous, was himself just getting
by. (Einstein got the Nobel in 1921, and all the prize money, as he
promised, went to Mileva. It amounted to 121,572 Swedish krona. Worth
roughly $20,000 back then, it's not much today, and it wasn't that much
even in 1921. Nowadays, the prize is about $1 million.)
Mileva seems to have used their two boys, Hans Albert and Eduard
(nicknamed "Tete"), as a means of coercing funds from her estranged
husband, but the real villain of the story is Einstein himself, who was
never really cut out to be a husband or father. In the letters, Einstein
frequently apologizes for having to cancel out on planned visits and
such, and he seems content to simply blow kisses at them while coolly
blowing off Mileva's demands for money.
Later in the decade, we see letters to and from Einstein and his
soon-to-be second wife, Elsa. It's almost disgusting to experience
Einstein's kissy-kissy attitude with Elsa in these correspondences,
especially when one knows that this marriage was also a colossal
failure. Mileva was no beauty queen, but I could never understand
Einstein's attraction to that pudding of a woman, Elsa.
Anyway, I got mildly ticked off when I read Einstein's letter to Mileva
dated November 9, 1918 (also Weyl's 33rd birthday!), in which he impuned
all us noble engineers:
I am glad that Hans has an intense interest in
something. On just what it is directed is less important to me, even
if it is engineering, by God!
The nerve of the guy!
PS: Einstein's insult to the engineering profession backfired on him.
Hans Albert Einstein went on to become a noted professor of civil
engineering at UC Berkeley. Ha!
PPS: The letter, sent by Einstein without a return address, was opened
and read by a Berlin government censor, who threatened to withhold
future deliveries unless the address was clearly marked. Sounds very
similar to what's going on in this country today. |
|
Looking for Lulu -- Posted by
wostraub on Tuesday, June 20 2006 |

The other night Turner Classic Movies reaired the 1999 documentary
Looking for Lulu, a great one-hour overview of the life and works
of American silent film actor Louise Brooks (1906-1985), whose character
Lulu in the 1928 German classic Die Büchse der Pandora
(Pandora's Box) is said to have enraptured Adolf Hitler long before
Marlene Dietrich or Eva Braun came along. I'll bet anything Hermann Weyl
and Albert Einstein for once agreed with Hitler on something (however,
Hitler subsequently denounced the film itself as "degenerate art").
I saw the film years ago at the old Vagabond Theatre in Los Angeles and
fell head over heels for this lady, whom I consider to be easily the
most beautiful film actor of all time. But she wasn't just a pretty face
-- she was a child prodigy, educated in classical literature from an
early age, and a gifted classical dancer with an equally brilliant mind.
In her early films she played a typical 1920s "flapper," but soon left
for Germany to seek more demanding roles. In Germany she was known as
Schwarze Sturzhelm (Black Helmet) because of her unusual
coiffure.
Amazon sells the documentary DVD for $90. I burned it on DVD
from the TCM airing and will send it out for a nominal fee if you're
interested, provided I don't get inundated by hundreds of requests. Drop
me a line.
PS: Pandora's Box is currently unavailable in Region 1 (USA)
DVD format, and Kino Video does not plan to release it anytime in the
near future. If you live in the UCLA area, you can attend a free
screening of the film at the Armand Hammer Museum at 8 pm on July 7,
2006.
Update:
The Criterion Collection will release the digitally remastered
Pandora's Box on American region DVD on November 10, 2006. It
will include four different musical soundtracks, the Looking for
Lulu documentary, stills, an interview with Brooks, and other
extras. |
|
Feynman's Wheels -- Posted by
wostraub on Tuesday, June 20 2006 |
 While
purging files from my Powerbook today, I came across a couple of
pictures having to do with Caltech physicist Richard Feynman (I don't
remember where I got them, but they must be fairly old, as the guy died
in 1988). Anyway, here is his license plate (I would have gotten
quanta for my plate, but we can excuse Feynman for the bad
spelling). While
purging files from my Powerbook today, I came across a couple of
pictures having to do with Caltech physicist Richard Feynman (I don't
remember where I got them, but they must be fairly old, as the guy died
in 1988). Anyway, here is his license plate (I would have gotten
quanta for my plate, but we can excuse Feynman for the bad
spelling).
This next shot of Feynman's van is interesting because it was obviously
taken while parked at the Dorothy Chandler Pavilion in downtown Los
Angeles. How do I know that? Because the tiered building in the
background is the home of my old employer, the Department of Water &
Power!

It doesn't show up very well, but Feynman's van is covered with
paintings of (appropriately enough) Feynman diagrams. I wonder
which auto detail shop in Pasadena did that (I might get something
Weylian for my Prius).
Today's Factoid: The DWP has a really neat engineering library on the
fifth floor, and I looked out from that vantage point one day many years
ago to see then-Mayor Tom Bradley standing with Queen Elizabeth in the
Pavilion right across the street. You don't see that every day! |
|
Fourth Order -- Posted by
wostraub on Friday, June 9 2006 |
One of Einstein's
objections to Weyl's theory of the combined gravitational/electrodynamic
field was that Weyl's field equations were of fourth, not second, order
in the metric tensor gμν and its derivatives.
However, variation of the fourth-order Weyl action
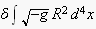
with respect to the metric tensor for empty spacetime gives
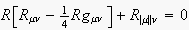
where the subscripted bar and double bar notation indicates partial and
covariant differentiation, respectively. It is relatively easy to show
that this differential equation has a non-trivial solution only when the
Ricci scalar R is a non-zero constant; the second term then
vanishes, and R can be divided out of the remainder, leaving a
term of second order. The surviving term can be solved (it's almost the
same as Schwarzschild's solution), giving the familiar expressions for
the advance of Mercury's perihelion, the deflection of starlight, etc.,
provided R is taken as a small constant.
The great Austrian physicist Wolfgang Pauli was aware of this
calculation as far back as 1921 (when he was just a 21-year-old kid),
and noted that Weyl's theory was just as capable of explaining the
perihelion shift and light deflection as was Einstein's theory.
The Schwarzschild-like solution includes a small repulsion term
(proportional to R) that might have something to do with the
observed accelerated expansion of the universe. Numerous researchers
have linked this term to the cosmological constant.
It is also interesting that Weyl's theory gives an Einstein tensor with
a 1/4 term (rather than 1/2). This makes it automatically traceless, a
desirable feature that Einstein himself searched for in vain. No wonder
Weyl thought he was really on to something! |
| Ray
Davis Dead at 91 -- Posted by
wostraub on Saturday, June 3 2006 |
Raymond Davis, the
Brookhaven/University of Pennsylvania physical chemist and 2002 Nobel
Laureate who devised accurate neutrino detection and counting methods,
has died at his Blue Point, New York home. He was 91.
Davis, whom I wrote about on this site a few months ago, showed
conclusively that the number of neutrinos (elementary particles first
anticipated by the work of Hermann Weyl) reaching Earth from the sun is
only one-third the number predicted by the standard solar model
developed by the late astrophysicist John Bahcall (and a close friend of
Davis). It was learned in the 1980s that the three types of neutrino can
morph into one another, so out of 100 solar neutrinos emitted by the
sun, only one-third will still be solar neutrinos by the time they reach
Earth. In an amazing case of theoretical/experimental jousting, both
scientists were proved to be right!
At the time of Davis' Nobel Prize in Physics, Bahcall said of his friend
Ray is not only an extraordinary scientific person,
but also an extraordinary human being. Ray treats the janitor in the
laboratory with the same friendliness and respect that he does the
most senior scientist. And for that, he is loved by his colleagues.
Davis is survived by his wife of 57 years, Anna.
|
|
Hermann Weyl and Imaginary Length -- Posted by
wostraub on Saturday, June 3 2006 |
Mathematical
symmetries, like Hermann Weyl's gauge symmetry, are essentially
undetectable aspects of action Lagrangians. This is the essence of all
mathematical symmetries. For example, the electromagnetic four-potential
Aμ has no absolute value -- an arbitrary gradient
can be added to it without changing Maxwell's equations. Before the
advent of the gauge revolution in physics, it was thought that the
four-potential therefore has no intrinsic meaning, and that the electric
and magnetic fields E(x) and B(x) represent the only
true reality. Nowadays we know better; E(x) and B(x)
are themselves composed of various derivatives of Aμ
which, though "undetectable" in a real physical sense, is the true
underlying reality. To paraphrase Columbia University's Brian Greene,
trying to determine the absolute value of Aμ is
tantamount to trying to figure out if the number 9 is happy.
Those of you who studied complex analysis in school may recall the
theory of residues, which provides a means for evaluating certain
improper integrals by integrating around the singular pole in the Argand
plane. Probably the first problem you solved involved the "single pole"
integral
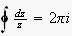
where z is a complex quantity and i is the imaginary
number (-1)1/2. It is interesting to note that
Einstein's objection to Weyl's gauge theory can be avoided by an appeal
to this pathetically simple equation if we identify z with the
(variable) length of a vector L under parallel transplantation
in a Weyl manifold. In fact, the German mathematical physicist Fritz
London used this equation in 1927 to derive the quantized radii of
orbital electrons for the Bohr atom in a Weyl space.
The only downside is that quantities such as vector length L
and the four-potential itself become essentially imaginary quantities in
Weyl spacetime. This observation has interesting consequences, and
perhaps the most profound consequence is that Weyl's theory has validity
only in quantum mechanics (where imaginary quantities are de rigeur),
not geometry. If you have followed this site at all, then you already
know that in 1929 Weyl successfully applied his gauge concept to quantum
theory, where it now represents one of the most profound ideas in all
modern physics.
But there are some researchers (and they keep emailing me!) who insist
that imaginary vector length is ok provided the square of the
length L2 always comes out real (reminiscent of the
probability interpretation of the square of the wave function Ψ2,
which is real). Well, I still don't know about all this, but I keep
thinking about it. If one always gets L2 when doing
a physical measurement, its complex or imaginary aspects are totally
hidden from us because we always just take the square root, thinking
that it, too, is real. For example, the square root of the real quantity
|z|2 is not +/- z, but a +/- ib,
where a and b are real numbers.
I'm an idiot, it's true, but you have to admit it keeps one's mind off
the moronic (and criminal) antics of President Bush, whose mind (and
legitimacy as a human being) are pure imaginary but whose crimes are all
too tragically real. |
|
Hermann Weyl and Steve Martin -- Posted by
wostraub on Saturday, June 3 2006 |
The comedian Steve
Martin, who was a philosophy major at California State University at
Long Beach (my undergraduate school!), once said that he learned just
enough philosophy there to screw him up for the rest of his life. I was
luckier than he was -- not only have I never taken a class in the
subject, it wouldn't have made any difference anyway, because I just
don't get philosophy at all.
Stanford University Professor of Philosophy Thomas Ryckman does get it
and, more importantly, one of his specialties is the relationship
between the development of general relativity and the state of German
philosophy in the early 20th century. He has written a book on the
subject,
The Reign of Relativity, in which both Einstein and
Weyl play prominent roles. Einstein himself was an armchair philosopher,
but Weyl was much more active on the subject. He was an early adherent
of the great German philosopher Edmund Husserl, and in fact married one
of Husserl's students, Helene Joseph.

Both Weyl and his wife were not only good philosophers, they were gifted
linguists. In the preface to his seminal book The Classical Groups:
Their Invariants and Representations, Weyl tells us
The gods have imposed upon my writing the yoke of a
foreign tongue [English] that was not sung at my cradle.
(Weyl wrote this in English, not German, and it has
always been one of my favorite quotes of his.)
Anyway, back to Ryckman, who in January 2001 gave a lecture at Berkeley
on the influence of Husserl on Weyl's gauge idea. I will not pretend
that I understand the philosophical part, as my brain is not really
wired for it (and it's not a chronic "senior moment" thing for me,
either; like pure math and mathematical logic, it just plain escapes
me). But Ryckman's talk did provide a pretty good introduction to Weyl's
gauge principle, and you just might understand the rest of it as well,
especially if you have ever studied transcendental phenomenology
or logical empiricism (whatever the hell they are).
Here is Ryckman's lecture in Microsoft Word format:
Article
|
|
Absolute Truth in an Age of Lies -- Posted by
wostraub on Tuesday, May 30 2006 |
In a letter to
Einstein dated 19 May 1918, Hermann Weyl asserted
As a mathematician, I must absolutely insist that my
geometry is the true, local geometry [reine Nahegeometrie];
the fact that Riemann posited only the special case Fμ ν
= 0 has no substantive legitimacy other than a merely historical one
... If in the end your views are correct concerning the actual
world, then I would regret having to accuse the dear Lord of a
mathematical inconsistency.
Einstein himself once stated that if his theory of
general relativity (gravitation) was not correct, he would have pitied
the Lord for having overlooked such a beautiful idea. This is what sheer
truth and beauty does to a person -- it is so compelling that it takes
on almost divine qualities, even to scientists who are otherwise devoid
of any religious faith. In the purest of examples, it is completely
objective, overriding any issues of ego or self-righteousness.
Another case in point: I am rereading The Physics of Immortality:
Modern Cosmology, God and the Resurrection of the Dead by the noted
astrophysicist Frank Tipler (he's the same guy who proved that an
infinitely-long rotating cylinder could be used as a time-travel
device). I am looking at it again only for the mathematics, which may or
may not be relevant to the author's central thesis -- that religion is
actually a branch of physics, and that we will all be resurrected to
eternal life by God when the universe reaches the so-called Omega
Point some umpteen zillion years from now. As a newly-minted PhD in
1976, Tipler was a diehard atheist until he experienced an epiphany of
sorts while playing with Einstein's gravitational field equations.
Whether one completely agrees with Tipler or not is beside the question
(as a Christian, I do not, but the stuff's interesting nevertheless).
The main point is that mathematical and physical truth has a beauty to
it that transcends much of what one experiences in day-to-day living.
Part of that truth (at least for me) is the realization that God exists
and had a purpose for putting us here in the first place (either as Adam
and Eve or as a couple of enlightened Australopithecines). I'm
not always sure he did the right thing, considering the mess we've made
of the world, but that's another story.
Weyl's own Road to Damascus occurred in 1918, when the concept of gauge
symmetry sprang into his mind. Einstein's was in the period 1913-15,
when he realized that another symmetry -- spacetime invariance -- could
be used to develop a theory of gravity. Both men were absolutely
convinced that they were in possession of the truth, and it changed
their lives forever.
I often ask myself what inspires or moves other people. Is it absolute
truth, or what they themselves believe to be the truth based on what
others have told them? How can we recognize absolute truth, and not be
fooled by others (or ourselves) that that truth is not in fact a lie? To
me, the only path is math and science, in combination with the teachings
of Jesus Christ, because these things cannot lie. But not everyone finds
math and science to be very interesting. Can truth be found in
accounting, economics, politics, American Idol or auto
mechanics? Can truth be found in the New Testament if mathematics and
physics are ignored? The answer is very clear to me, but who am I to
impose my beliefs on others? |
|
Gravitational Lensing of a Quasar -- Posted by
wostraub on Thursday, May 25 2006 |
This amazing
photograph, taken by the Hubble Space Telescope, shows a cluster of
galaxies (about 7 billion light-years distant) splitting the image of a
single very distant quasar (about 10 billion LY away) into no fewer than
five images (the bright bluish-white points of light near the photo's
center). The galaxies act as a gravitational lens that
imperfectly reproduces the quasar's image in a circular arc about the
galactic field of view.

The photo also shows distorted images of galaxies near those responsible
for the lensing. Quasars (quasi-stellar objects) are themselves
the cores of galactic-sized objects containing super-massive black
holes. The extreme luminosity of a quasar is powered by matter being
accreted into the hole; as it spirals in, friction from the accretion
heats the matter up to the point where intense x-ray and gamma radiation
comes pouring out. Quasars were originally a great mystery to
astrophysicists because their great luminosities didn't seem to agree
with their extreme distances.
Another example of God's miracle universe. Sadly, the Bush
Administration, in its hatred and fear of legitimate science, has cut
funding for the Hubble Space Telescope, whose orbit will eventually
decay until it burns up in Earth's atmosphere. On the plus side, the
money saved will be available to help fund new wars of aggression for
oil and other dwindling resources, but in the name of truth and justice
and liberty and Christian goodness. But hey, whaddya want, America --
buck-fifty gasoline or a geeky orbiting science project? |
|
Reality v. Formalism -- Posted by
wostraub on Sunday, May 21 2006 |
In the preface to his
1917 book The Continuum, Hermann Weyl tells us
It is not the purpose of this work to conceal the
bedrock on which the house of analysis is founded with a fake wooden
structure of formalism -- a structure which can fool the reader and,
ultimately, the author himself into believing that [formalism] is
the true foundation. Rather, I shall show that this house is,
to a great extent, built on sand.
Weyl goes on to say that the then-popular use of
arithmetic and irrational number theory to solve the problem of the
continuum should be stamped (sarcastically) with the title
Pythagoras. Therein lies the seed of Weyl's thesis: much of real
analysis at the time was based on circular logic; it was non-rigorous,
and therefore corrupted by false or meaningless formalism. In his book,
Weyl set out to make things right.
Today we have a few people around who are brilliant in both modern
mathematics and physics; Witten, Penrose and Baez come immediately to
mind. But Weyl was the first of this kind to come upon the scene.
Trained initially as a mathematician, he immediately ventured out into
physics, where he made many profound and fundamental discoveries.
Weyl was not afraid to attack what he perceived as either unintentional
misrepresentation or outright lies. In his book he attempts to set
straight issues that at the time contradicted unquestioned mathematical
thinking that greats like Dedikind had established decades earlier.
Later, when Weyl proposed his theory of the combined
gravitational-electromagnetic field, he did not back down even when his
theory was questioned by the great Einstein. Weyl's persistence, which
was based on a firm conviction that what he had proposed was based in
absolute truth and beauty, paid off when he applied his theory to the
then-emerging field of quantum mechanics. Weyl's gauge principle stands
today as one of the most profound tenets of quantum physics.
Who today has the courage to go up against established authority? Today
we are told lie after lie by our political leaders, and we swallow every
one of them, hook, line and sinker. Who among us has the courage to tell
Bush and Company that they are liars and false prophets?
Weyl denounced Hitler, but had to flee his beloved Germany in 1933
because neither he nor all his brilliant contempories could stem the
tide of nationalistic insanity that was sweeping the country. Not long
afterward, magazines and posters were displayed with Einstein's photo
and Noch ungehängt! (not yet hanged) all over Germany. Not
surprisingly, Einstein too fled the country. A dedicated Nazi effort to
discredit the theories of special and general relativity soon had the
German people thinking they had been tricked into believing a lot of
intellectual hokum. Books were burned, ideas themselves were banned, and
the great edifice that was once Deutsche Mathematik und Physik
was destroyed in favor of ignorant, arrogant nationalism.
Sadly, this is America today. But the danger is heightened infinitely by
America's possession of 10,000 nuclear bombs, spy satellites that can
watch and record everything we do and say, a hatred of legitimate
science and truth, and a crazed, fanatical, nationalistic Christian
millennialism that wants desperately to hasten Armageddon through
unilateral, preemptive war.
It is ironic that today Weyl and Einstein would almost certainly be
forced to return to Germany to escape the fascist madness that has
overtaken our country.
This is "circular logic" of a most disturbing kind. God save us all.
|
|
Einstein -- Collected Papers -- Posted by
wostraub on Monday, May 8 2006 |
I spent several hours
at Caltech today perusing its copy of the Collected Papers of Einstein
(writings and correspondence, nine volumes, with a few English
translation versions). I went there to copy Einstein's correspondence
with Hermann Weyl, only to realize that I already have most of it.
But I was unprepared for the sheer volume of Einstein's correspondence
with other notables of the time. Letters in those days (this was 90
years ago) was the email of their time, and Einstein must have spent a
fair amount of his free time just writing letters.
Particularly interesting are the letters to Mileva (his ex-wife) and son
Hans Albert, all of which show varying degrees of the man's emotions,
including warmth, concern, impatience, intractitude, and even a little
hostility. Though he genuinely cared for his two sons (in 1903 he and
Mileva had an out-of-wedlock daughter, Liserl, who was given up for
adoption), Einstein was not a family man, and his boys must have
suffered for it. Hans went on to become a professor of civil engineering
at Berkeley (he developed the Einstein bed load function in
sedimentation theory), while Eduard had mental problems all his life and
died at an early age. The fate of little Liserl is a mystery.
The Collected Papers abounds with correspondence between
Einstein and hundreds of notable scientists, mathematicians,
philosophers and political scientists. It's well-organized and makes
fascinating reading, if you've got the time. It's also available for
purchase, but each volume runs around $100, which is far beyond my
pocketbook.
As for Weyl, Einstein and my favorite mathematical physicist wrote to
each other dozens of times, discussing many different topics, including
Weyl's gauge theory and related/unrelated mathematics, gravitation
theory, philosophy, German politics, the war, and what kind of salaries
professors should be given. Weyl was also the frequent subject of
Einstein's correspondence with others. It very much takes you back to a
time when it appeared that Einstein's relativistic theories (and
generalizations) would eventually solve all the standing problems in
physics (this was before quantum theory, of course). |
|
Wilczek on Weyl -- Posted by
wostraub on Friday, April 28 2006 |
| In October 2005, MIT's
Frank Wilczek, the winner of the 2004 Nobel Prize in Physics (for
discovering the principle of quark asymptotic freedom), wrote a nice
tribute to Hermann Weyl.
Here it is in .PDF format. |
|
Einstein v. Weyl -- Posted by
wostraub on Wednesday, April 26 2006 |
Partly as a means of
ridding my mind of the preposterously immoral state of this country and
the criminal actions of the Bush Administration, I'm writing a brief
synopsis of the argument that Einstein and Weyl had regarding Weyl's
early metric gauge theory.
Several people have written in, asking what was behind Einstein's
objection to the theory, was it valid, did they remain friends, etc.
Hardly the appropriate subject matter for the general public, but the
story itself is fairly interesting, and I hope I can do it justice. I'm
getting ready for a trip, but I'll try to have it up in the next few
days. |
|
Derivation of the Weyl Conformal Tensor -- Posted by
wostraub on Wednesday, April 12
2006 |
Some time ago I
mentioned the Weyl conformal tensor, which is fundamental to the
understanding of gravitational tidal effects. Whereas Einstein's
equation (which involves only the Ricci tensor and scalar) describes
gravitational compression and compaction of matter (volume reduction via
gravitational attraction), the Weyl tensor is responsible for the
deformation of matter, with the initial volume of matter remaining
intact. For example, if you ever happen to fall into a black hole, your
body's volume will be retained but you'll be increasingly squished
sideways and elongated in the direction of the hole. This rather
unpleasant phenomenon, known to black hole afficionados and the
cognoscenti as spaghettification, is due to the Weyl conformal
tensor. Why God allows black holes to exist is anybody's guess (maybe
just because they're fascinating).
How did Weyl discover this tensor? I could never find out. He seems to
have simply written it down (he was that good).
Numerous people have asked me how the tensor can be derived. Since I've
never seen the derivation, I'd never done the calculation, at least
until now. It's much simpler than you might think.
The file conformal.pdf is on the menu
to the left. |
|
Weyl and the Question of Asymmetric Time -- Posted by
wostraub on Thursday, April 6
2006 |
What really interests me is whether God had any
choice in the creation of the world. --
Albert Einstein
In the early 1920s, Hermann Weyl discovered a new tensor
quantity (the Weyl conformal tensor) which is basically the
Riemann-Christoffel curvature tensor with the contracted pieces (the
Ricci tensor and scalar) removed. The resulting tensor is conformal
(angle preserving) as well as metric gauge invariant. Weyl must have
come across the tensor while investigating the consequences of his 1918
gauge theory and its presumed (but wrong) unification of gravitation and
electrodynamics, but I have been unable to confirm this.
The Weyl curvature tensor is zero for flat spacetime, but for curved
manifolds it is non-zero, even in the absence of matter. The tensor is
responsible for gravitational tidal effects, in which (say) a
spherical collection of particles is contorted into a prolate
ellipsoidal shape (although the tensor preserves the initial volume). In
fact, Weyl curvature is responsible for the tidal bulge in the Earth's
oceans caused by the moon's gravitational pull. By contrast, the Ricci
curvature terms deform matter by gravitational compression, and volume
is not preserved.
In 1979, the British mathematical physicist Roger Penrose (also a gifted
science writer) announced the Weyl Curvature Hypothesis, which
essentially states that the Weyl tensor was precisely zero when the Big
Bang occurred and will become infinite if and when the controversial Big
Crunch occurs. On the basis of this hypothesis, Penrose believes that
time must be asymmetrical; that is, time proceeds from the Big Bang to
the Big Crunch in only one direction. This contradicts the CPT theorem,
which basically states that physics is also valid for reversed time
(that is, all equations remain valid if we replace t
with -t ). The laws of physics may be time
direction-invariant, but on a universal scale this might not be the
case. Penrose believes that a consistent quantum-gravity theory
(assuming we ever come into possession of it) will demonstrate that the
direction of time is really only one-way.
Whether the universe will end in a Big Crunch is debatable (current data
indicate that the universe will continue expanding forever), but what is
certain is that much of the matter in the late universe will coalesce
into black holes. Spacetime curvature near the event horizon of a black
hole is highly Weylian, so even if Penrose is wrong the totality of Weyl
curvature in the late universe will undoubtedly be extremely high if not
infinite.
I've mentioned Penrose before. He has two excellent (and very readable)
books out: The Emperor's New Mind (Penguin Books, 1989) and
The Road to Reality -- A Complete Guide to the Laws of the Universe
(Knopf, 2004). The latter book is a life-altering text that should be
read by everyone who has even the slightest interest in physics, the
universe, and God's role in it all. Buy this book, read it carefully,
and then place it next to the Bible and Hamlet on your
bookshelf; you will then be able to call yourself an enlightened member
of the human race.
The Weyl Curvature Hypothesis provides a direction for time's arrow, and
is therefore intimately connected with the increase of entropy in the
universe (as demanded by the second law of thermodynamics). Indeed,
Stephen Hawking and others have proved mathematically that the surface
area of a black hole's event horizon is proportional to the hole's
entropy. Thus, in the late universe, the level of entropy contained in
black holes will be enormous. By comparison, the entropy of spacetime at
the time of the Big Bang was very low, if not exactly zero. Thus, the
Big Bang and Big Crunch are distinctly different events. This calls into
question the reality of a "cyclic universe," that is, one that comes
into existence and then recollapses over and over.
I think Weyl would have been pleased that his curvature tensor is today
profoundly associated with the fate of the universe and related unsolved
problems in modern physics. |
|
Inflation Theory Getting Dissed -- Posted by
wostraub on Sunday, March 19 2006 |
After the Washington
Post's article on cosmic inflationary theory came out a few days ago
(and discussed by me below), a veritable raft of conservative idiots
have come out of the woodwork proclaiming that it's just nonsense:
I just hate it when the media reports carefully
vetted scientific data as fact and not as just one of many valid
points of view. I'm not asking for them to ignore the opinions of
these so-called scientists, but they really should report the fact
there's a lot of controversy about whether this kind of evidence is
valid. LIke, were you there, huh, Mr. Hotshot Washington Post? As if
this ludicrous nonsense - a marble blows up like a baloon [sic] to
become the entire universe in a trillionth of a second - is more
plausible than Genesis? Give me a break!
To be fair, it doesn't help things when the WaPo reports
that the "universe expanded from the size of a marble to the expanse of
the entire cosmos in a trillionth of a second." This is just plain
wrong, but I think conservatives would have a problem with the article
even if it had been reported accurately.
Alan Guth's inflation theory says that about 10-35 seconds
after the Big Bang, the universe began to expand at an exponential rate.
This increased rate of expansion lasted until about 10-30
seconds after the Bang (a total duration of very nearly 10-30
seconds). During this expansion, the volume of the still-infant universe
increased by a factor of some 1050. Expand something the size
of a marble by that factor, and you get a marble the size of a globular
cluster -- big, but still quite tiny compared to the size of the
universe today.
But I think conservative young-Earth creationists still have problems
with this. To them, there was nothing until God created it a scant 5,000
years or so ago. Adam and Eve rode to work on dinosaurs (they actually
believe this), and all animals were herbivorous (even T. rex,
who needed those fangs and claws to get through the notoriously chewy
plants that grew back then). Then came the Fall of Mankind, when some
animals literally became evil and began to eat their more peaceful
cousins. What utter, puerile nonsense! "Where were you when the Big Bang
occurred?" seems to be their standard question to cosmologists these
days. Well, you creationists weren't around either -- so there, idiots.
I think a good part of the problem can be traced to the use of terms
like "millionths of a millionth of a trillionth of a second." These
terms are almost meaningless when taken out of context. I recall when my
high school physics teacher told us about Planck's constant, which is
roughly 6 x 10-34 joule-sec. My first thought was "Hell,
that's practically NOTHING. Anything that small is really no different
from ZERO." But I couldn't have been more wrong! The problem seems to be
related to the fact that humans cannot imagine something as small as a
decimal point followed by 33 zeros and the number 6.
Similarly, many people have a hard time imagining even a trillionth of a
second, which is much larger. "How could anything happen in a millionth
of a millionth of a second?" they ask. Well, an unstable particle that
has an average lifetime of that long is what particle physicists call a
very long-lived particle. Most unstable particles exist for much shorter
periods. Some are around for only 10-20 seconds.
The 10-35 second following the Big Bang is on the same level
of smallness as Planck's constant. If you want, we can sit here and talk
about tiny numbers all day long -- how about 10-1000 seconds?
Me, I can't even begin to imagine such small numbers. And I'm stupid at
both ends -- I can't imagine what infinity looks like, either.
But I know they exist.
What do I believe? If anybody really gives a damn, I believe that at
t = 0, God said "Let's have a quantum fluctuation take place in
this boring, expanseless nothing of a universe and get something
interesting going." BANG. Later, he created creatures with wonderful
minds that could actually calculate what the early universe MIGHT have
looked like.
And, for better or for worse, God also created creatures that did not
want to use their minds. These he called "Republicans," although in the
early days they went by the names Pharisees and Sadducees.
|
|
Inflation Theory Verified? -- Posted by
wostraub on Friday, March 17 2006 |
New data from the
Wilkinson Microwave Anisotropy Probe (WMAP), a satellite launched in
2001, has provided scientists "smoking gun" proof that the so-called
Inflationary Universe, first proposed by astrophysicist Alan Guth in
1981, is correct.
The data provide much finer details of the distribution of the cosmic
microwave background (CMB), which is an "echo" of the Big Bang. The CMB
was first detected in 1965 as a uniform, isotropic radiation
representing a universal thermal background of about 2.73o
Kelvin, or 2.73 degrees above absolute zero. [Note: the "degree" label
o for Kelvin temperatures is always suppressed, so it's just
2.73 K.]
The microwave radiation "echo" actually occurred about 270,000 years
after the Big Bang. Why is that? It's because prior to that, the
expanding ball of ionized plasma and intense radiation was so opaque
("thick") that light from within couldn't get out. At around t = 270,000
years the fireball had cooled to the point where the plasma became
transparent, and THERE WAS LIGHT!
Later data and refinements showed that the background radiation is not
quite uniform, but "granular." This graininess was predicted by Guth's
theory, but proof of the theory had eluded scientists until now. The
figure below is WMAP's map of space showing cooler (blue) and hotter
(red) regions (the temperature gradients are truly small, on the order
of a fraction of a Kelvin). Numerous scientists have remarked that
looking at the map is akin to looking at the face of God.
The inflationary theory states that the Big Bang, which occurred very
nearly 13.7 billion years ago, began as a uniform expansion of spacetime
which then accelerated briefly (and by briefly, I mean on the order of
10-30 seconds). This brief expansion, now almost jokingly
called the "Inflationary Epoch," was due to fluctuations in what is
believed to have been the false vacuum of the early stages of the Big
Bang.
Columbia University's Dr. Brian Greene, a renowned astrophysicist, has
called the findings "spectacular and "stunning," while Dr. Michael
Turner, assistant director for mathematics and physical sciences at the
National Science Foundation, called the data "absolutely amazing."
Meanwhile, concerned Republicans are scrambling to figure out how the
universe could be 13.7 billion years old, when everybody knows that God
created it only 5,000 years ago. Earlier today, there were indications
that Senate Majority Leader Bill Frist would propose a bill that would
nullify the WMAP data and imprison, torture and execute the study's
research scientists as godless, freedom-hating terrorists. But President
George W. Bush, who subsequently inquired about the cosmic microwave
background himself, remarked "If that there kozmick microwave is a new
kind of meat cooker, then I'm all fer it." |
| The
Fly in the Cathedral -- Posted by
wostraub on Wednesday, March 15 2006 |
I just finished
reading Brian Cathcart's excellent 2004
book The Fly in the Cathedral (Farrar, Straus and
Giroux, publishers), which describes in detail the discoveries of
Rutherford (the atomic nucleus), Chadwick (the neutron), and Cockcroft
and Walton (induced atomic fission). The book's title refers to a
comment made by Rutherford, whose original atomic "plum pudding" model
gave way to the correct view of a tiny, lone nucleus sitting in the vast
empty space of the atom -- like a fly in a cathedral.
But the bulk of Cathcart's book is taken up by the story of John
Cockcroft and Ernest Walton, who in early 1932 bombarded lithium metal
with accelerated protons. It is an intriguing tale of frustration,
dashed hopes, personal tragedy, and ultimate victory. The scientists'
apparatus, Neanderthal by today's standards, continually broke down,
adding months to their efforts (and always overshadowed by lack of funds
in those early days of worldwide depression). But their efforts were
repaid many times over -- they ultimately found to their utter amazement
and delight that protons could split lithium-7 -- a stable element --
into two helium atoms. The Cockcroft-Walton experiment was the very
first experimental observation of man-made atomic fission, the
transmutation of one element into another, the first splitting of the
atom.
The experiment also offered the very first practical test of Einstein's
E = mc2 formula. The observed 8.5-MeV energy of each
product helium nucleus balanced the books with respect to the reactant
particle energies. Like Einstein had said in 1905, mass and energy are
truly equivalent! In recognition of their work, the Nobel Committee
awarded Cockcroft and Walton the 1951 Nobel Prize in Physics.
The book's decription of Cockcroft/Walton's discovery is nothing short
of heartwarming, but it also includes tragedy. At the time of their
triumph, both men lost infants to childhood disease, tragedies that
nearly destroyed the men and their wives in spite of their
groundbreaking discovery.
But Cathcart saves the best for last. Ernest and Frieda Walton had a
long, happy marriage, and they went on to have four more children who
all pursued careers in science (three in physics!) Meanwhile, John and
Elizabeth Cockcroft went on to have five more children -- a scientist,
an engineer, a priest, a nurse, and a teacher.
God be praised! |
| The
Anthropic Principle -- Posted by
wostraub on Wednesday, March 15 2006 |
For a long time I've
been planning to put up an article on the Anthropic Principle,
which purports to offer some proof that an intelligent, omniscient
entity (let's call it God) really did engineer the universe for our
benefit. There's actually quite a bit of evidence that such a principle
is scientifically valid, but, until I get around to it, here's one of
the more convincing arguments.
The Big Bang, which occurred about 13.7 billion years ago, started out
basically as a super-hot plasma of quarks and leptons. But within 2
minutes this plasma had cooled sufficiently to allow for the formation
of protons and neutrons. Using Boltzmann's equation and the fact that
neutrons decay into protons, electrons and antineutrinos (the life of an
unbound neutron is about 15 minutes), it can be shown that the expanding
fireball at age 2 minutes was composed of about 75% protons and 25%
neutrons (with relatively minor concentrations of other stuff). Thus,
three-fourths of the universe consisted of hydrogen, the basic fuel of
star formation via nucleosynthesis.
Gravity gradually coalesced clouds of matter into spheres and compressed
them to the point where nuclear fusion began in their cores. Almost all
of this fusion involves the creation of helium nuclei from hydrogen.
This is the kind of fusion that mankind is now trying to duplicate for
long-term energy generation.
But after a few billion years, many stars burn up their supplies of
hydrogen. A star begins to cool, contracts further under gravity, and
then the core heats up again as a result of the increasing pressure. The
temperatures eventually get so high that the star's helium can fuse into
carbon, oxygen, neon and several other low-atomic weight elements. Some
of these stars eventually explode as novas and supernovas, and their
supplies of carbon, oxygen, hydrogen and other trace elements is what
makes up all living things. All living things on Earth owe their
existence to stardust flung out by ancient star explosions. Humans, for
example, are composed of about 20% carbon and 65% oxygen, a reflection
of the equilibrium battles in the sun involving these two elements.
During the helium-burning phase of a middle-aged star, there are three
primary reactions going on that affect the formation of carbon. One is
the triple-alpha reaction, in which three helium nuclei fuse to
form a carbon-12 nucleus. The carbon formed in this process, however,
can be scavenged by another process in which a helium nucleus fuses with
a carbon nucleus to form oxygen-16. At the same time, oxygen-16 can also
be scavenged by a helium nucleus, yielding neon-20. It turns out that
the rates of these competing reactions and the physical constants that
determine their equilibrium points are very finely tuned; if the excited
states of carbon-12 and neon-20 nuclei were only slightly different,
all middle-aged stars would evolve atmospheres that are either
oxygen-rich and carbon-poor or composed predominently of neon. The
physics of these processes, including a few minor ones that take place
simulaneously with those I've described, have been worked out by
astrophysicists over the years to a gnat's eyebrow. If the
fundamental physics of the elementary particles making up carbon,
oxygen, helium and neon were displaced by only a few parts per million,
life could not exist anywhere in the universe. Thus, the universe
as we know it must have been designed, or we wouldn't be here.
However, some physicists have argued that, if the many-worlds
interpretation of quantum physics is valid, then our universe is just
one of an infinite number of possible universes in which the physics
happened to be "just right." In the vast majority of these other
universes, the physics is "off" and life does not exist. In this way of
thinking, a designer God would not be necessary because life exists here
because of a statistical fluke.
But this argument is flawed. The processes I described above represent
only a single example of the Anthropic Principle. There are many other
processes that are also finely tuned for the existence of life, and the
totality of these processes makes the statistical argument really hard
to accept. I have estimated that, given the totality of "life-favorable"
physical processes and constants, on average only one such universe
would arise out of 1040 universes. While I suppose this is
still statistically possible, it seems much easier just to admit the
existence of God. In my mind, these numbers imply that the
non-existence of God is statistically about one in 10-40.
To me, that's essentially zero.
So get over it -- God exists! Whether he/she/it is Jehovah, Allah or
Brahma is purely a matter of faith. And I'll leave it at that for now.
Post Script -- Speaking of faith, where do a lot of Americans derive it?
I recall about a year and a half ago a grilled cheese sandwich that sold
on eBay for $28,000. Why? Because it had what appeared to be the figure
of Jesus Christ on it (the pan it was cooked in was subsequently
auctioned off for $20,000). Since then, I've heard of trees, pancakes,
highway overpass stains, and hotcross buns that appeared to depict
Christian figures. All of these events made a big splash in the media,
and literally thousands of people made pilgrimages to these "holy"
sites. Yet the average American knows nothing at all about the
scientific Anthropic Principle, which to me represents the only rational
way of looking at physical "proof" of God's presence.
Americans truly are idiots. |
|
Saunders MacLane and Mathematics Under the Nazis -- Posted by
wostraub on Sunday, March 12 2006 |
While researching some
notes on Hermann Weyl’s tenure at Göttingen during the period 1930-33, I
came across a story involving the American mathematician Saunders
MacLane of the University of Chicago. MacLane was a gifted 1930 Yale
mathematics graduate who wanted to further his studies by attending the
best graduate school in the world. This led him, in 1931, to the
Mathematics Institute at the University of Göttingen in Germany, which
was then universally regarded at the finest school of its kind. Its
previous and then-current mathematics instructors included the likes of
Gauss, Riemann, Dirichlet, Klein, Minkowski, Courant, Hilbert, Noether,
and Weyl.

MacLane’s arrival at the university coincided with the turbulent
political, economic and social scenario that was plaguing Germany at the
time. It would shortly result in the demise of the Weimar Republic and
give rise to Adolf Hitler and the Nazi Party.
Hitler was appointed Chancellor of Germany on 30 January 1933. A month
later (27 February) the Reichstag (German parliament) building was set
on fire, supposedly by a member of the German Communist Party, but most
probably by a mentally ill transient (who was quickly executed).
Regardless of the real cause, the Nazis used the incident to foment the
fear that social and liberal radicals in the country wanted to overthrow
the government.
Their first step was to enact the "Reichstag Fire Decree" (Reichstagsbrandverordnung)
in March 1933, which nullified many of the key civil liberties of German
citizens set forth in the country’s constitution. With Nazis already
occupying prominent positions in the government, the decree was used as
a legal tool to suppress publications deemed unfriendly to the Nazi
Party. It also allowed the Nazis to imprison anyone considered to be in
opposition to their policies and actions. The decree is generally
considered to be the Nazis’ first major effort to establish a
dictatorial, one-party German state.
However, the Nazis feared that the Reichstag Fire Decree would be
insufficient to bring about total control of the country. Consequently,
on 23 March 1933 they engineered the Reichtag's passage of the "Enabling
Act" (Ermächtigungsgesetz). This act provided the Nazis the
means of establishing total dictatorial control by legal mandate,
because now Hitler and his Nazi-dominated cabinet could enact laws
without interference by (or even participation of) the Reichstag.
The formal name of the Enabling Act was the "Law to Remedy the Distress
of the People and the Reich" (Gesetz zur Behebung der Not von Volk
und Reich). Cleverly worded as such, the German people were quickly
brought on board Hitler’s plan to protect them through harsh (but
seemingly benevolent) means.
The Nazis’ third step was to implement Article 48 of the Weimar
Constitution. In reaction to the instability that arose in Germany
immediately following its defeat in World War I, the government had
amended the constitution to provide for emergency powers that might be
needed to quell public unrest, insurgency, and the possibility of civil
war. Article 48 was implemented via the "Order of the Reich President
for the Protection of the People and the State" (Verordnung des
Reichspräsidenten zum Schutz von Volk und Staat). Under the
provisions of the article, Hitler and his cabinet acquired essentially
unlimited power in Germany, all done legally and within the constraints
of the constitution. This effectively ended the Weimar Republic.
Germany, now officially a dictatorship, thus inaugurated the Third
Reich.
Now back to MacLane who, in early 1933, was working under the guidance
of Göttingen assistant professor Paul Bernays. He knew Weyl well, and on
one occasion attended a dance party that Weyl and his wife gave at their
apartment. Though the political strife made life uneasy, these were
heady times for the young MacLane, who regularly came into contact with
the greats of contemporary German mathematics. He even came into the
presence of Hitler and Hermann Göring at an opera, but acknowledged
later that he failed at the time to recognize the inherent evil in these
men. MacLane later thought about how he might have changed history if
he'd carried a pistol that night!
On 7 April 1933, following the country’s short but complete takeover
just a month earlier, all Jewish professors (along with everyone not
considered totally committed to the National Socialists) were summarily
fired. By month’s end Courant, Noether, Neugenbauer, Bernstein, Bernays,
Hertz and Lewy were drummed out of the university. MacClane, forced to
seek a new advisor, went to Weyl, who took him on. MacClane subsequently
received his doctorate in the summer of that year, just prior to Weyl’s
decision to leave the country as well (Weyl was a Christian, but his
wife had a Jewish background, so their two sons were considered to be
Jewish).
So, by the summer of 1933 the world-renowned Mathematics Institute of
the University of Göttingen had been decimated. A total of 18 professors
had been forced to leave. A similar fate befell other universities
across the country.
MacLane returned home with his wife, Dorothy, in August 1933. In his own
words, he had personally witnessed “the damage done to academic and
mathematical life by any subordination to populism, political pressure
and proposed political principles.”
MacLane ended up at the University of Chicago, where he received many
awards for his work in mathematics, especially algebraic logic. He died
in 2005 at the age of 95.
I bring up this little story because I see what I consider to be an
irrefutable parallel between what happened to Germany in 1933 with what
is happening in my own country today. By the latter part of 2001,
President George W. Bush, an unsuccessful, uncharismatic, witless,
incurious, unrecovered alcoholic, was well on his way to an inglorious
one-term presidency. In his first eight months in office he had
accomplished nothing of any importance, and his approval ratings were
well below those of his unpopular, one-term father, George Sr. Then came
September 11.
The Pentagon and Twin Towers attacks, like the Reichstag fire, breathed
new life into Bush’s foundering presidency. And like the Enabling Act
and the enactment of Article 48, the ridiculously-named "Patriot Act"
and the recently uncovered governmental domestic spying scandal have
given Bush and his zealots unprecented, almost dictatorial power. And,
like in Germany in 1933, the American people have bought into the lies
of the Bush Adminstration because they’ve been taught to be afraid.
What we’ve seen from Bush since 9/11 is an unremitting horror of illegal
war, missing WMDs, legalized killing, torture, imprisonment, secret
back-alley meetings and deals to benefit the corporations, environmental
destruction, astronomical deficits, wiped-out surpluses, degraded civil
liberties, hatred of objective scientific inquiry, mega-capitalism and
materialism, and unbelievable religious hypocrisy. The United States,
thanks to Bush, is today almost univerally hated around the world.
I’m going to make a prediction before I close this overly-long diatribe:
I predict that within a year we will hear about a new scandal involving
illegal Bush Administration spying on the election plans of the
Democratic Party. While Nixon couldn’t pull it off because what he did
was deemed illegal and immoral (even by Republicans), such niceties
simply do not carry weight any more under the Bush Reich.
May God save this country. Even so, come Lord Jesus.
PS - You can download a five-page PDF document of MacLane's personal
reminiscences of Göttingen at
MacLane.pdf |
| "Ich
fahre nach Pasadena ..." -- Posted by
wostraub on Sunday, March 5 2006 |
Here's a brief
letter (along with its English
translation) that Einstein wrote just prior to his second visit to
Pasadena in 1931. In it, he lauds America's love of science and its
ability to balance production and consumption.
How times have changed. Americans now prefer superstition, video games
and celebrity worship to math and science, while our gluttonous material
appetite threatens to consume the entire world.
Exactly where and when he wrote this (and to whom) is anybody's guess.
Like it? You can have it for only
$23,000. |
|
More on Neutrino Oscillations -- Posted by
wostraub on Sunday, February 26
2006 |
Many people have
written to say that they were fascinated by last week’s PBS program on
neutrinos, The Ghost Particle. It is interesting to note that
Hermann Weyl also made fundamental contributions to our understanding of
these particles, which may be the most numerous things in the universe.
In his seminal 1929 paper, Electron and Gravitation (Zeitschrift
f. Physik, 330 56), Weyl was the first to recognize that the
treatment of spin-1/2 particles (like the neutrino) in a gravitational
field requires a covariant derivative that is appropriate to fermionic
fields.
Weyl’s development of the spin connection ω abλ
and the associated spin covariant derivative emerged from this work, as
was his recognition that the zero-mass version of the Dirac relativistic
electron equation allowed for a description of particles that violate
parity (this is practically the de facto definition of the neutrino!)
While Weyl’s paper preceded Pauli’s 1930 neutrino hypothesis by a year
(and it is doubtful that Weyl had any inkling about the existence of
this particle at the time), his work nevertheless provided a sound basis
for the neutrino’s subsequent mathematical elucidation.
Weyl also was totally unaware of the existence of three types of
neutrino or the possibility of neutrino oscillation, which was
the subject of the PBS program. Whatever the physical process behind a
neutrino’s penchant for converting itself into any of the three types,
it is abundantly clear that a successful description will involve the
dynamics of fermionic fields against a gravitational background, and
this will by necessity involve Weyl’s spin connection and derivative.
Not bad for a mathematican who was once scolded by Pauli for straying
into the physics community!
Several people have asked me about more advanced yet readable
information on neutrino oscillation. I’m the wrong person to ask,
because I know practically nothing! But there are several papers I’ve
collected that have helped me understand the things a tiny bit:
Dieter Brill and John A. Wheeler, Interaction of Neutrinos and
Gravitational Fields (1957). Reviews of Modern Physics,
29 465. [This is probably the first article you should seek out.]
C.Y. Cardall and George M. Fuller, Neutrino Oscillation in Curved
Spacetime: A Heuristic Treatment (1997). Physical Review D,
55 No. 12, 7960.
Xin-Bing Huang, Neutrino Oscillation in de Sitter Spacetime.
arXiv:hep-th/0502165 v1 (12 February 2005).
Victor M. Villalba, Exact Solutions to the Dirac Equation for
Neutrinos Propagating in a Particular Vaidya Background (2001).
International Journal of Theoretical Physics, 40 No. 11,
2025. |
| The
Ghost Particle on PBS -- Posted by
wostraub on Tuesday, February 21
2006 |
I hope you all caught
The Ghost Particle on PBS tonight. The ghost particles are, of
course, neutrinos, first postulated by Wolfgang Pauli in 1930. Nearly
massless and traveling close to the speed of light, approximately 100
trillion pass through your body every second, and "pierce the lover and
his lass," to quote the famous John Updike poem.
The program chronicles the search for the solar neutrino, and focuses on
the initially-contradicting data between experiment and theory. First
came the theory, proposed by John Bahcall in 1964, that electron
neutrinos would be produced by the sun at a rate of X per
second. Then Ray Davis and colleagues built an apparatus that could
actually measure the things. Strangely, their observations indicated
that the sun was producing neutrinos at the rate of only X/3.
Scientists around the world couldn't figure out just who was right (if
either).
The Standard Model of particle physics says that electron neutrinos are
massless and travel at the speed of light. But in the 1970s and 1980s
two more neutrinos showed up -- the muon neutrino and the tau neutrino.
Today, the family consists of electron neutrinos, muon neutrinos and tau
neutrinos, along with their antimatter counterparts. Most physicists
believe that no new neutrinos will ever be found.
Anyway, to make a long (but very fascinating) story short, it was later
discovered that the three kinds of neutrinos can randomly oscillate
from one kind into another. Thus, the number of solar electron neutrinos
reaching Earth is reduced by a factor of two-thirds. Bahcall's theory
was vindicated, as were Davis' experiments. Both physicists
were right!
Because neutrino oscillation requires that these particles have a
non-zero proper time measure, neutrinos cannot travel at the speed of
light, so they must have a tiny but non-zero mass. Consequently, there
was early conjecture that neutrino mass might account for the "missing
mass" in the observed universe (the total number of neutrinos in the
universe is almost unimaginable, so even a tiny mass would add up to
something truly significant). However, it is now believed that other,
more exotic forms of non-baryonic matter make up the vast bulk of the
known universe's mass-energy. Oddly enough, the ordinary matter that you
and I know and love (protons, neutrons, electrons, hamburgers, etc.)
accounts for only about 5% of the "stuff" of the universe. The rest is
"dark matter" and "dark energy." Very odd, indeed.
Although Davis (now in his 80s) is suffering from Alzheimer's disease,
he was fully cognizant back in 2002 when, to the delight of his family
and fellow researchers, he won the Nobel Prize in Physics for his
neutrino work. He was accompanied in Stockholm by no fewer than 23
ecstatic family members -- wife, children and grandchildren. God be
praised!
I recorded this excellent PBS program on DVD-R. Let me know if you'd
like a copy. |
|
Weyl's Take on the Gravitational Energy-Momentum Tensor -- Posted by
wostraub on Friday, February 17
2006 |
Shortly after
Einstein's November 1915 announcement of his general theory of
relativity, Weyl attempted to derive a coordinate-invariant form of the
energy-momentum tensor that expressed conservation via an invariant
divergence formula. His failure to find a fully-covariant expression of
this tensor puzzled many physicists at the time. And despite repeated
attmepts over the years by many scientists, no one has discovered a
satisfactory form of the tensor.
This is very odd, because general relativity is practically the de
facto definition of invariance theory, yet something as
conceptually simple as gravitational energy-momentum conservation
continues to elude us.
Weyl's attempt is documented in the first edition of his 1918 book
Space-Time-Matter (Raum-Zeit-Materie). It's a mess, if only
because of the inconsistent index notation he used in those days. But,
yes, a divergenceless energy-momentum tensor can be written down (it
looks like T μν + t μν)
but the quantity t μν is really only a
pseudotensor -- it's not invariant with respect to a change in the
coordinates, and it's not even symmetric with respect to the indices.
This is very frustrating!
Long ago, I thought it might be possible to use Weyl's φ-field
to derive a truly covariant form of the energy-momentum tensor. I failed
in this attempt, but I'm little better than a total idiot, so it's still
possible that this approach is valid. Something to think about on an
otherwise cold and rainy night. |
|
Spin Connection -- Posted by
wostraub on Saturday, February 11 2006 |
| I rewrote The Spin
Connection in Weyl Space (a somewhat pretentious title, I know) and
included an elementary overview of vector parallel transfer and
covariant differentiation. The .pdf file is posted on the menu to the
left. The typos are all fixed now (I think), but I'm washing my hands of
the whole thing, as it still doesn't read the way I wanted it to. Enjoy
it if you can. |
|
DPGraph -- Posted by wostraub
on Monday, January 30 2006 |
 Years ago when I was
teaching, I used a simple but powerful program for creating static and
animated computer graphics called
DPGraph. If you have ever attended university, chances are the
program can be downloaded for free (the site has a list of hundreds of
site-licensed universities, and all you have to do is click on yours [be
honest, now] and the program is automatically downloaded gratis).
You can also buy the thing outright for just $10. Either way, it's a
bargain, and it's a blast. Years ago when I was
teaching, I used a simple but powerful program for creating static and
animated computer graphics called
DPGraph. If you have ever attended university, chances are the
program can be downloaded for free (the site has a list of hundreds of
site-licensed universities, and all you have to do is click on yours [be
honest, now] and the program is automatically downloaded gratis).
You can also buy the thing outright for just $10. Either way, it's a
bargain, and it's a blast.
Just enter a 2-D or 3-D algebraic expression on the command line, toss
in a few parameters, and the program gives you fantastic graphics. It's
used by countless schools (including elementary, middle and high
schools), but with a little imagination you can easily create
exceedingly-complex graphics and animations that look like output from a
graduate institution.
The program, which only takes up about 500 KB on your hard drive, will
run on any Windows OS (it also runs on my Mac Powerbook via Virtual PC,
but Virtual PC is such a dog that very high-resolution graphics
[especially animated graphics] take a long time to generate).
The program's documentation is minimal; there's no manual, but the HELP
menu should provide all the information you'll ever need. Also, the
DPGraph website has many hundreds of free downloadable graphics files
that serve as useful examples of the required programming.
DPGraph is a far cry from professional programs like Wolfram's
Mathematica, but that's overkill for most people, anyway (it's also
a far cry from my old Keuffel & Esser sliderule, but that's another
story, and I don't want to date myself too badly here). |
|
"Now We're All Sons of Bitches" -- Posted by
wostraub on Thursday, January 26
2006 |
These were the words
of physicist Kenneth Bainbridge to J. Robert Oppenheimer, director of
the Manhattan Project, immediately following the successful test of the
atomic bomb at Alamogordo, New Mexico, on July 16, 1945.
Why my renewed interest in JR? I was looking over a copy of a letter
Weyl had sent to Oppenheimer in 1934, and Weyl practically pleaded with
"Oppie" to accept the directorship of the recently-founded Institute for
Advanced Study (IAS) in Princeton. But Oppenheimer repeatedly begged
off, thinking that he "would be useless" in such a place.
At the end of the war, with Germany defeated and Japan reeling under two
atomic blasts and the concurrent deaths of 225,000 civilians, both Weyl
and Einstein felt that Oppenheimer was no longer suitable for the IAS
job, and they campaigned for Wolfgang Pauli (who also happened to win
the Nobel Physics Prize that year). Nevertheless, Oppie got the job in
April 1947, where he was to remain almost 20 years until his death in
early 1967.
My search for a Weyl-Oppenheimer association led me to what is currently
considered the definitive study of the "father of the atomic bomb" in
the new book American Prometheus: The Triumph and Tragedy
of J. Robert Oppenheimer by Kai Bird and Martin J. Sherwin (Alfred
A. Knopf, 2005). The book has little to say about Weyl (who never worked
at Los Alamos), but it gives a detailed account of the life of
Oppenheimer, his early academic triumphs, his success at Los Alamos, his
attempts to internationalize the science of nuclear weapons to prevent a
cold war, the subsequent trials he endured as a suspected Communist
sympathizer and national security threat, and his later life, which he
devoted to sailing, writing, and quiet intellectual pursuits.
True to their nature, the Republicans demonized Oppenheimer as a
peacenik and threat to US unilateral nuclear dominance. Eisenhower had
Oppie's security clearance revoked, and the scientist was scarred by the
McCarthy commie witch-hunt of 1953. It was not until the Democrats had
regained power in 1960 that the US government attempted to patch up its
pathetic relationship with him, and he was eventually awarded numerous
honors and medals by presidents Kennedy and Johnson. It was too little,
too late. Oppenheimer died on 18 February 1967 of throat cancer, much
disillusioned but accepting of his fate.
I remember reading Oppenheimer's obituary in a Time magazine at
my high school library. "Father of the Atomic Bomb" is about all I
remember of it. Later, the noble and wise administrators at Duarte High
School staged an assembly with a guest speaker who spoke to us of the
benefits and charms of fascism and communism. This went on for some
time, while the students all booed and hissed. Only then did the speaker
reveal himself to be a true American patriot whose speech was a sham
designed to expose the manifest evils behind communistic indoctrination.
We all cheered. (I remember this as if it were yesterday.)
While reading the book (I have two other books on Oppenheimer, but this
one's the best), I realize that it's 1953 all over again. Science is
being disparaged, superstition is on the rise, crooked and corrupt
politicians are again in power (perhaps permanently this time), and
Americans have gone into a deep, deep sleep. The warnings of scientists
like Einstein, Weyl, Oppenheimer, Bohr, Serber and many others have been
totally ignored, and as a result the world is far more dangerous today
than ever before. A corrupt, moronic president, in league with a corrupt
but very clever and ambitious Republican Party, false Christians all, is
leading us down the path to destruction. Sons of bitches, indeed.
|
|
Collapse -- Posted by wostraub
on Sunday, January 22 2006 |
Take a test tube, fill
it with sterilized nutrient broth, add a few bacteria, and incubate. The
bacteria will multiply exponentially. Their waste products will also
accumulate, and at some point the organisms will enter lag phase, then
undergo death. The bacteria, being insensate organisms, don't know any
better. As long as there's a supply of food and nutrients, they'll
reproduce without any consideration of the possible consequences until
either the food is gone or their wastes destroy their environment.
I've just finished reading Jared Diamond's Collapse: How Societies
Choose to Fail or Succeed (Viking Press, 2005). Diamond, a
professor of geography at UCLA, is a physiologist, evolutionary
biologist, and a biogeographer (whatever that is). He's won numerous
awards for his science and writing, including the MacArthur Foundation
Fellowship. He's also the author of the Pulitzer Award-winning Guns,
Germs and Steel. He is a writer to be reckoned with, and this is a
fantastic book.
Collapse decribes the rise and fall of human cultures and
societies like the Easter Islanders, the Maya, the Norse Greenlanders,
the Icelandic Vikings, and our own Southwest American Anasazi. Each one
prospered thanks to plentiful natural resources, but their populations
invariably grew to the point where their respective diminished
environments could no longer support them, and they quickly died off.
Each tells the almost identical story of how population growth destroyed
the cultures' resilience to withstand climate change and periodic
drought. Without exception, each was the victim of a successive pattern
of overextension and environmental destruction, followed by denial,
resource wars, disillusionment, despair and even, near the very end,
cannibalism.
Diamond's first case is the Eastern Island Polynesians, who came to this
remote island (about 2,300 miles due west of Chile) around 900 AD. The
island was small but heavily forested, including a species of vanished
tree called the giant Chilean palm. Birds abounded, as did fish and
shellfish, and the islanders eked out a fairly comfortable living on a
diet based on limited agriculture, local birds, fish, and even
porpoises. For whatever reason, the islanders began a program of
competitive monument building, consisting of huge stone statues called
moai and even larger stone support foundations called ahu.
An extinct volcanic pit furnished an igneous rock that was easily
carved, and the islanders built roads upon which they transported their
massive statues by sheer muscle power. The local giant palms, with
heights and diameters of up to 100 feet and 7 feet respectively,
provided the construction materials needed to build the elaborate system
of primitive levers, cranes and ramps required to raise the statues.
Over time, many hundreds of statues were built.
Within a few hundred years, the forest was completely gone. Erosion
wiped out what little arable soil the islanders had. The birds and
porpoises left, and the fisheries were wiped out. The natives, desperate
for food, turned to cannibalism. All this is irrefutably recorded in the
island's trash heaps and burial mounds.
Ironically, in the last days the few remaining islanders overturned
and/or destroyed the statues, perhaps out of rage that their priests and
elders had deceived them and led them down the path to destruction.
Diamond muses over what that unnamed Easter Islander might have been
thinking as he cut down the island's last tree:
Like modern loggers, did he shout "Jobs, not trees!"?
Or "Technology will solve our problems, never fear, we'll find a
substitute for wood"? Or "We don't have proof that there aren't
palms elsewhere on Easter, we need more research, your proposed ban
on logging is premature and driven by fear-mongering"?
To this Diamond might also have added "Don't worry, our
gods won't fail us, the Rapture is coming, and we'll all be saved."
[BTW, for those of you who believe the Rapture is going to bail you out,
you should recall the conversation Jesus had with Satan in Matthew
4:5-7.]
Diamond's book goes on to talk about modern cultures and how many are
following in the exact same footsteps as the above-mentioned ancient
peoples. He gives a few positive examples, like the Japanese, whose
series of islands is still 94% forested, but he overlooks the fact that
the Japanese are preserving their forests by cutting down everyone
else's.
After checking this 570-page book out from the library, I simply could
not put it down, and read it into the wee hours until I was finished.
Diamond is a first-rate writer, and his narratives flow like prose. The
subject material is so appropriate to the here and now that Collapse
should be required reading for all high school and university students.
My only criticism of the book stems from its title, which implies that
cultures can choose to fail or succeed. In my opinion, Diamond does not
give an adequate description of how such decisions can be made, or even
if there's evidence that today's cultures are engaged in such
decision-making. As for me, the whole concept of rational
decision-making lies solely in the minds of people who have been
unfairly labeled liberal, God-hating pessimists. Sadly, the world is
ruled by capitalist exploiters who still think that the Earth's
resources are inexhaustible.
I personally see no evidence that Earth's governors are deciding
anything. In spite of our sentience and ability to alter our fate, I
fear we're really no different than bacteria. |
|
Deep Down Things -- Posted by
wostraub on Friday, January 20 2006 |
Seduced by the glowing
reviews of UC Santa Cruz physicist Bruce Schumm's new book, Deep
Down Things (Amazon, about $19) and, curious over the fact that the
book devotes almost 80 pages to an elementary elucidation of gauge
theory, I bought the thing and read it.
First off, the book is pretty much aimed at the motivated lay reader who
wants to understand the non-mathematical particulars of the Standard
Model of the electromagnetic and strong and weak nuclear forces (he
wisely left gravity out of the loop because it's clearly beyond the
scope of a book of this kind). The book includes rather extensive
(though elementary) expositions on topics such as Lie groups and Lie
algebra, SU(2) and SU(3) isospin and hypercharge symmetries, the weak
interaction and the quark model, and by book's end I had regained much
of what I invariably tend to forget about this stuff.
However, the book is inconsistent at the levels with which it treats (or
should treat) complex numbers, quantum mechanical phase invariance, and
related topics. For example, Schumm writes down Schrodinger's
one-dimensional wave equation on numerous occasions, explaining what all
the parts represent, but he doesn't feel that the reader is quite up to
understanding the exponential version of complex numbers. This lack of
confidence extends to his description of phase invariance, in which nary
a e i θ appears in the book. This is a shame,
because anyone who has even a smidgen of knowledge about z = a + ib
knows that the exponential form (known as Euler's relation), which is
ubiquitous in quantum mechanics, is easier to use and more intuitive.
You cannot explain to someone what a unitary operator is with z!
Schumm's description of gauge invariance, Weyl's brainchild, is
particularly muddled. The principle of gauge symmetry is easy to
understand, but not if you leave the basic math out of the discussion.
The book's last chapter, Into the Unknown, discusses a few
advanced opics, along with the Higgs field and physicists' hopes to
discover it with the European Large Hadron Collider, which is scheduled
to go into operation in 2007. And while Schumm plays down the role of
gravity in all this, he hints at the possibility that a unified theory
of all four forces will radically change the way we think of everything.
The problem with Schumm's book is the same one that plagues all
popularized expositions of modern physics theories -- there is precious
little middle ground that these writers are willing to explore between a
non-mathematical, golly-gee treatment and a higher-level textbook-like
approach. In my opinion this is not Schumm's fault, but rather that of a
dumbed-down reading public coupled with a rather cynical attitude of the
publishers. |
|
What a Waste -- Posted by
wostraub on Monday, January 16 2006 |
Here's a morality play
masquerading as a physics problem.
You no doubt know that controlled nuclear fusion would solve the world's
energy problems for all time. Fusion is really very simple -- just get a
deuterium atom and a tritium atom (these are available or easily-made
isotopes of ordinary hydrogen) close enough, and they'll fuse to form
helium-4 (along with a left-over neutron), with the release of lots of
energy. How hard can it be to get two tiny nuclei close to one another?
Well, it's deceptive -- the Coulomb repulsion between the particles is
so great that only truly enormous confinement temperatures and pressures
can get them to fuse. While this has actually been done in gigantic
experimental machines (like the Tokamac), the energy expended in the
experiments far outweighs the energy derived from fusion. Scientists are
still trying to achieve "breakeven," and as a result practical nuclear
fusion is still many decades away.
But there's another way that doesn't require huge pressures and
temperatures.
Take a deuterium-tritium (DT) ion with a single shared electron. Fire a
muon into the ion (the muon is an elementary particle that is identical
to the electron, but about 207 times as heavy). The muon knocks the
electron out of the DT pair and begins to orbit the nuclei, just like
its electron counterpart did. But because of its greater mass, the mean
orbital radius of the muon is 207 times smaller than that of the
electron. This causes the deuterium and tritium nuclei to move very
close to each other. The muon's small orbital radius also effectively
shields the positive Coulombic repulsion of the DT nuclei, which gets
them in even closer. Within a few thousandths of a nanosecond the nuclei
undergo fusion, with the release of about 17.6 MeV of energy. The muon
is unharmed during the fusion event and leaves the helium-4 in search of
another DT pair, where it can do its trick all over again. Because the
muon comes out unscathed, this process is called muon-catalyzed
fusion. It has been demonstrated many times in laboratories over
the past three decades.
So what's wrong with this picture? Nothing, but there are a few
technical problems that have to be overcome. One, muons have to be
created, you can't buy them in stores. They come from decaying negative
pi-mesons (or pions, π-), and you need a linear
accelerator to get the necessary pions. Second, the muon is itself
unstable and decays into an electron, a muon neutrino and an
anti-electron neutrino (a muon has a typical life of only 2
microseconds). And third, once a muon catalyzes a fusion event, it often
develops the habit of hanging around the helium-4 nucleus once it has
formed. In view of the muon's short lifetime, this "stickiness" of the
muon wastes valuable time.
However, the first and second difficulties are not all that critical --
they can be dealt with. The most critical problem is the muon's tendency
to loiter around and be unproductive. A means for making unsticky muons
would represent a truly profound discovery and a wonderful gift to
mankind's future welfare.
There's even another particle just like the electron and the muon called
the tau (τ-), which is about 17 times heavier than the muon.
Tau-catalyzed fusion might someday be demonstrated, although
the tau's lifetime is about ten million times shorter than the muon's.
So what's the upshot of all this? Every year, the world's nations spend
nearly $1 trillion for weapons of war (about half of this amount is
spent by the United States). Recent estimates (by the 2001 Nobel prize
winner in economics, no less) of the actual out-of-pocket costs of the
Iraq war total about $2 trillion
Article. Forgetting annual US defense expenditures, what do
you think we could have done with $2 trillion? Develop practical muon-catalyzed
fusion, maybe? It boggles my mind to think that the US might be able to
develop non-polluting nuclear fusion energy generation if it would only
get its head out of its ass!!
This is just another of President Bush's outrageous legacies -- at a
time when Peak Oil is rapidly approaching, and the country is in
desperate need of an alternative energy source, Bush decides that what
we really need to do is monopolize (i.e., steal) the world's remaining
oil resources! This cannot save us, because even if Europe, China, India
and the other developing countries can be held at bay, the resulting
destruction of the world's economies will also destroy ours. And my
guess is that the other countries of the world wouldn't stand for it --
remember, Russia still has 6,000 nuclear weapons and the missiles to
deliver them.
Make no mistake about it -- the lunatic US Emperor George W. Bush is the
most dangerous man in the world, and we tolerate him at our extreme
peril. |
|
Cosmic Landscapes -- Posted by
wostraub on Sunday, January 15 2006 |
In his new book
The Cosmic Landscape: String Theory and the Illusion of Intelligent
Design (Amazon, about $16), Stanford physicist Leonard Susskind
suggests that the universe we inhabit is only one of a nearly infinite
number of "megaverses," perhaps as many as 10500. Each of
these possible universes is based on a different set of fundamental
physical constants, so one universe may permit life while another does
not.
Susskind, a leading string theorist, does not necessarily imply that
intelligent design is wrong, it's just that in his multiverse theory
there's no need for it. Given an almost infinite number of possible
universes, it is inevitable that at least one universe will look just
like the one we live in. And there we are!
For the same reason, Susskind feels that things like beauty and elegance
are also inevitable, especially when a universe contains thinking
creatures. This would seem to imply that there is no such thing as
"absolute truth," which is abhorrent to me, but it's still something
worth thinking about.
Is it possible to flip an "honest" coin 10500 times in a row
and have it come up "heads" each time? Of course! The probability is
very small, but it's not zero. If there are a similar number of
universes out there, all orthogonal to the one we inhabit, the chances
are good that just about any kind of otherwise implausible event or
condition will be observed.
Are these universes the "many mansions" that Jesus spoke about? Susskind
would probably disagree, but I argue that it's equally possible that it
is.
Meanwhile, purely for your enjoyment, here's the Sombrero Galaxy (M104),
located about 50 million light years away from us in the constellation
Virgo. This beautiful galaxy is just one of the hundreds of billions
known to exist in our one universe. God be praised!
 |
|
Embracing Lies as Truth -- Posted by
wostraub on Saturday, January 14
2006 |
I haven't read James
Frey's A Million Little Pieces, and I never will, but I have to
comment on Frey's appearance on Larry King Live three nights
ago. The fuss centers around accusations that Frey's "redemption" is
based on the many lies and half-truths contained in his book, and the
fact that Oprah Winfrey had championed his book on her book club. The
book sold well as a result, but the allegations are pushing sales beyond
Frey's wildest dreams.
Anyway, Winfrey herself called in to King's show to defend Frey and the
book (and her own reputation). Instead of admitting that she had made a
mistake by trumpeting a liar's work of fiction, she made two incredible
claims -- that the book's publisher was to blame for any untruths in the
book, and that she and Frey had apparently created a "new genre" of
legitimate literature, a pleasant blend of fact and fiction. The ancient
adage about turning a sow's ear into a silk purse comes immediately to
mind.
By the way, Frey also brought his mommy along to the King show, no doubt
to throw added weight onto the lies he was spinning.
Anyone who believes Frey's nonsense is a boob, and I guess that includes
Oprah as well as most Americans, many of whom have actively campaigned
to have Winfrey run for president. Winfrey herself seems to be
self-delusional, thinking that her billions are proof that she's
infallible. But the real blame falls on a celebrity-intoxicated American
public that cannot differentiate between truth and lies anymore.
It's no wonder Bush is president. |
|
Teach Quantum Physics in the Churches? -- Posted by
wostraub on Thursday, January 12
2006 |
Today, two opposing
members of the Ohio Board of Education appeared on Lou Dobbs Tonight
to present their respective cases for and against the teaching of
intelligent design in Ohio public schools.
Although ID suffered a stinging defeat in Pennsylvania last month, its
adherents are regrouping and taking their arguments to school boards in
numerous states -- Ohio, Georgia, Missouri, Kansas, and even California.
Dobbs listened to both sides, and at one point actually suggested
teaching quantum physics alongside evolution in the schools! He then
asked if it would be proper to teach comparative religion in public
school. The pro-ID guest disagreed, and implied that religious education
had no place in the schools. My read on this is that ID supporters would
try to quietly introduce Christian education into public schools via the
teaching of ID. Apparently, IDers are sold on the idea that intelligent
design belongs solely to the Christian faith; comparative religion be
hanged. I have yet to see a Jew, Muslim or Buddhist demand that ID be
taught as a scientific discipline in public schools.
PBS' Frontline is currently running a series (Country Boys)
on the problems of rural youth -- lack of jobs, premarital sex,
methamphetamine abuse, depression, etc. Last night's episode took us
into a rural Kentucky high school classroom where the teacher ridiculed
evolution as anti-God pseudo-science: "Did Jesus Christ look like an
ape? Do you think you came from a bunch of monkeys? That's not what I
believe!" or words to that effect. I really felt sorry for the school's
students, who undoubtedly have enough problems in their lives. Now they
can add ignorance to the list.
I really like the idea of teaching quantum mechanics (at the appropriate
level) in churches, because QM is undoubtedly one of the tools God uses
to run his universe. Like religion, QM is based on numerous postulates
that cannot be scientifically proven, and so have to be taken on FAITH.
Everyone believes in QM, because modern life could not be possible
without it. Why can't the IDers look at evolution the same way?
Evolution is just one of God's tools to ensure the perpetuation of the
planet's species.
But, as Lou Dobbs surmised today, ID ain't going away, and it will
continue to itself evolve until it is absolutely disproven as a science
and banned outright or legitimized and made a mainstay in the public
schools. Hopefully, the legitimization of ID, like evolution, will also
take millions of years. |
|
Fascinating Physics -- Posted by
wostraub on Saturday, January 7 2006 |
A hydrogen atom is
just an electron bound to a proton. What if you replace the proton with
some other positively-charged particle?
If that particle is an antielectron (or positron), you get
something called positronium, or Ps. Physics Today rightly
calls it "nature's simplest atom."
Electron/positron pairs are created near charged particles, but they
invariably annihilate one another, resulting in photon pairs. But under
the right circumstances, and for intervals on the order of 100
nanoseconds, they join to form Ps. There are two bosonic species of Ps:
ortho-Ps, in which the particle spins are aligned (spin one), and para-Ps,
in which the spins cancel (spin zero).
The latest issue of Physics Today (January 2006) reports that
researchers at the University of California at Riverside have found
indirect evidence that two Ps atoms can join to form a diatomic molecule
(Ps2). If confirmed, the researchers believe that they can
form a Bose-Einstein condensate at a temperature of around 15 degrees K.
This in turn might then lead to gamma-ray lasers in which each photon
has an energy of about 0.5 MeV. Amazing!
I imagine even George W. Bush will be interested in this, but for
another reason -- gamma-ray space lasers to zap the evil-doers (set your
weapon to deep fat fry, comrade!) |
| To
The Mall, Patriots! -- Posted by
wostraub on Saturday, January 7 2006 |
I laughed out loud
when I read Jesse Eisinger's WSJ article about neoconsumerism under the
Bush Reign of Terror. He calls it zombie consumerism -- for a
reason you'll need to read the article to understand.
Eisinger points out that for the first time since the Great Depression,
Americans spent more money in 2005 than they earned. This negative cash
flow greatly increased the nation's debt, as Americans flocked to take
out home equity loans to pay for all their SUVs, gadgets and credit card
installments (I guess they see this as "found money" that doesn't have
to be paid back). I peeked in on the Commerce Department's website back
in November, and it confirmed that Americans were indeed saving nothing
but spending nevertheless.
Eisinger warns that with the flattening of the real estate market,
record bankruptcy rates, usury-like credit interest rates, the spiraling
differential between workers' pay and lavish CEO pay, and the very real
connection between stock market performance and the availability of
consumer cash, the future bodes ill for Bush's wundereconomy.
WSJ Article
Can't afford food? Eat EQUITY!
EQUITY |
|
Weyl on Time Travel -- Posted by
wostraub on Saturday, January 7 2006 |
While slaving away at
the gym this morning, I started to think about time travel again. This
is one of my favorite topics, in spite of the fact that I really don't
think it's possible, at least for any massive object.
If you check out the New Testament, you'll see numerous references to
God and light. I believe this connection is more than just hyperbole,
because if God is purely spiritual then he undoubtedly moves on a
null geodesic, which is to say that he is free to move around just
like a photon of light.
A photon lives is a very strange world, indeed. Because its line element
vanishes (ds2 = gμν dxμdxν
= 0), it exists everywhere in the universe at all times -- past,
present and future. This fact is paradoxical to us humans, because when
we snap on a light, photons are created at that instant, and when they
are absorbed by our cornea, they are annihilated. Clearly, then, light
can be created and destroyed in a short time interval. But a photon's
own existence is much different -- to a photon, it is people
whose lives are sedentary and fleeting. This is nothing more than an
extreme example of Einstein's so-called twin paradox, which of
course is not a paradox at all when you've understood special
relativity. So the saying "God is light" is probably closer to the truth
than one usually imagines.
In 1994, the noted Caltech physicist Kip S. Thorne published his
wonderful book Black Holes and Time Warps -- Einstein's Outrageous
Legacy. Mostly a non-mathematical look at time travel through
wormholes and the like, it's a fascinating read that investigates
various time travel possibilities along with their inherent problems and
paradoxes. Following one of his promotional lectures (I think it was one
of the Leon Pape Lectures), I got the chance to talk to Thorne about
time travel, quantum field theory, relativity, and life in general. But
when I asked him if he himself believed in time travel, I got an elusive
answer.
[By the way, I took along a copy of Thorne's 1965 first book
Gravitational Theory and Gravitational Collapse. He signed it for
me, and told me that he still gets a miniscule royalty check from the
publishers each year from the half-dozen or so copies that they sell.]
Thorne and his British pals and colleagues Stephen Hawking and Roger
Penrose are arguably the world's foremost authorities on time travel.
But many years ago, our good friend Hermann Weyl also speculated on the
time-travel possibilities associated with a rotating universe:
It is possible to experience events now that will in
part be an effect of my future resolves and actions. Moreover, it is
not impossible for a world line (in particular, that of my body),
although it has a time-like direction at every point, to return to
the neighborhood of a point which it has already once passed through
... In actual fact the very considerable fluctuations of [the metric
tensor gμν] that would be necessary to produce
this effect do not occur in the region of the world in which we
live. Although paradoxes of this kind appear, nowhere do we find any
real contradiction to the facts directly presented to us in
experience.
In fact, Weyl took the rather extreme view that the very
concept of time is illusory and an inherent debilitation of the human
mind. He once famously remarked
The objective world simply is, it does not
happen. Only to the gaze of my consciousness, crawling
upward along the world-line of my body, does a section of the world
come to life as a fleeting image in space which continuously changes
in time.
Before you dismiss these words as overly metaphysical,
consider the remarks of St. Thomas Aquinas (or was it St. Augustine?),
who "knew what time is except when asked what it is." What really
is time? Einstein treated it as the fourth dimension, but it's obviously
not just another coordinate. My guess is that we will never really know
until we stand before God. But will time still exist then?
The concept of time not existing (which must have been the case "before"
the Big Bang) is not so far-fetched because if time doesn't exist there
can be no causal loops or other time-related paradoxes. A universe
without time might not be such a bad place. At least we wouldn't get old
and decrepit!
On a perhaps more realistic note, consider this. Let's say that you want
to travel back to Northside Square in Bolivar, Missouri at exactly 5:00
pm CST on November 5, 1955 (like Professor Brown in Back to the
Future). You get into your Way Back machine, set the dials on the
flux capacitor, and hit the "go" button. An instant later, you
materialize in the vacuum of empty interstellar space, where you quickly
decompress and die. What went wrong?
The problem is due to the fact that Earth was not at the location you've
traveled to in time. Because the Earth is rotating on its axis and
moving around in the solar system (which is also moving in the Milky Way
Galaxy, which is also moving relative to the Local Cluster), you don't
want a time machine. What you want is a spacetime machine, a
device that will take you both when and where you want
to go. This means that you have to know the precise spacetime
coordinates of your destination, otherwise you're likely to end up in
airless space or physically embedded in a tree or mountain. To get these
coordinates, you need to have the world line (4-D history) of the
travel-to location. But where are the world lines of all physical
objects and locations in the universe maintained?
I don't believe that UFOs are Little Green Men; I prefer to believe that
(if they exist at all) they are time-traveling historians or scientists
who, for whatever reason, prefer to remain undetected. If way-back time
travel is at all possible, future travelers in their spaceships will
know that it is far safer to approach Earth from space, where any
imprecision in their spacetime coordinates won't matter (unless they
happen to materialize within an asteroid, but then space travel is
an adventure, isn't it?)
The best reference I've found on the subject is the 1993 book Time
Machines by Paul J. Nahin, a professor of electrical engineering at
the University of New Hampshire. It's still available in paperback, and
it's excellent. |
|
Math and Physics Math - There's a Big Difference -- Posted by
wostraub on Wednesday, January 4
2006 |
Many years ago, I took
a graduate course on variational calculus. I had studied the same
subject in my math methods (for physicists) courses, and I thought I
would try out a pure math class for the hell of it. The material was
familiar stuff, so I thought it would be a snap.
Boy, did I get a surprise. The professor's chalkboard scribblings were
all in formal math notation, and it was a struggle for me from day one.
The professor seemed to delight in sticking it to the few physics
students that took the course. I ended up with a "B" for the class, my
worst math grade ever.
Over the ensuing years I have tried without success to understand pure
math. This is a damn shame to me, because it makes up the vast bulk of
Weyl's work. For the same reason, I've had difficulty following John
Baez's excellent but otherwise unintelligible online notes on higher
gauge theory (actually, anything that doesn't directly involve
physics gives me fits). My pure-math stupidity seems also to be the main
reason why I've had such a hard time understanding string theory.
I'm not giving up, but the time is rapidly approaching when I will do
just that. I just turned 57, so not only are my little grey cells
getting worn out, there's just not that many of them left now. And in
not too many more years, I probably won't give a damn about even
thinking anymore -- just like a Republican. |
|

 She did not forget Jesus!
She did not forget Jesus!







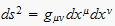
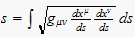 .
. 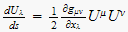
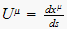
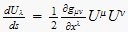





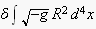
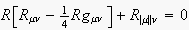
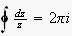




 Years ago when I was
teaching, I used a simple but powerful program for creating static and
animated computer graphics called
Years ago when I was
teaching, I used a simple but powerful program for creating static and
animated computer graphics called 