2012
Archives
| A Weyl Christmas, 1933 — Posted Friday, December 14 2012
|
 As I have related before, post World War I Germany was very liberal, Berlin in particular, and Hermann Weyl, German-born but teaching in Zürich
at the time, was himself quite caught up in the liberal spirit. While helping his close friend and fellow ETH colleague Erwin Schrödinger solve the
latter's famous wave equation in 1925, Weyl did double duty wooing Schrödinger's wife Anny (the Schrödingers had a famously open
marriage, and the 1933 Nobel physics prize winner developed his wave equation while "on sabbatical" in the mountains with another woman). And how
did Weyl's wife, Hella, feel about all this? She herself was fooling around with ETH physicist Paul Scherrer, probably with Hermann's knowledge, if not
approval. Liberal, indeed.
As I have related before, post World War I Germany was very liberal, Berlin in particular, and Hermann Weyl, German-born but teaching in Zürich
at the time, was himself quite caught up in the liberal spirit. While helping his close friend and fellow ETH colleague Erwin Schrödinger solve the
latter's famous wave equation in 1925, Weyl did double duty wooing Schrödinger's wife Anny (the Schrödingers had a famously open
marriage, and the 1933 Nobel physics prize winner developed his wave equation while "on sabbatical" in the mountains with another woman). And how
did Weyl's wife, Hella, feel about all this? She herself was fooling around with ETH physicist Paul Scherrer, probably with Hermann's knowledge, if not
approval. Liberal, indeed.
This story is examined in more detail in the 2009 book
Mind and Nature: Selected Writings on Philosophy, Mathematics, and Physics, which is arguably the best book available on Hermann Weyl (though with
the exception of the foreward, it's mostly a compilation of articles written over the years by Weyl himself).
The book is edited by physicist and musician Peter Pesic (St. John's College, Santa Fe, NM), who
writes
As Schrödinger struggled to formulate his wave equation, at many points
he relied on Weyl for mathematical help. In their liberated circles, Weyl remained
a valued friend and colleague even while being Anny Schrödinger?s
lover. From that intimate vantage point, Weyl observed that Erwin "did his
great work during a late erotic outburst in his life," an intense love affair
simultaneous with Schrödinger?s struggle to find a quantum wave equation.
But then, as Weyl inscribed his 1933 Christmas gift to Anny and Erwin (a set
of erotic illustrations to Shakespeare?s Venus and Adonis), "The sea has bounds
but deep desire has none." (Typical of Weyl to describe desire in the context of the "No Boundary" theory of cosmology.)
The book makes a great Christmas gift (Pesic's book, not the Venus and Adonis erotic folio), but I already have a copy. Readers compelled by
an overwhelming
desire to send me a gift should instead make a generous donation to their favorite charity.
|
| On Scale and Dimension, or, Size Doesn't Matter — Posted on Wednesday, December 12 2012
|
 I have ants in my pants today. Must be my imminent 64th
birthday (December 21) and the concurrent end of the world on that date, as the Mayans predicted. It's also the shortest and darkest day of the
year. Well, it's been a good life. I have ants in my pants today. Must be my imminent 64th
birthday (December 21) and the concurrent end of the world on that date, as the Mayans predicted. It's also the shortest and darkest day of the
year. Well, it's been a good life.
I took a graduate class in astrophysics in the 1970s, mainly because I was interested in astronomy at the time (though I was more interested in just
building telescopes, not really using them). I didn't get much from the class, but I managed to learn that the Big Bang wasn't just a singular
explosive event—it actually created space as it expanded outward (and it created the "outward" as well). Later I would learn that the observable
universe is almost precisely 13.75 billion years old, while the radius of the universe is about 47 billion light-years. How can that be? Even if the expansion
occurred at the speed of light, the radius could not be more than 13.75 light-years in extent. The explanation is that the universe we observe is also
creating space as it expands, so th
e relative velocities of distant galaxies (as determined by redshift data) cannot be used alone to
determine cosmological
distance scales. I recall thinking that issues of scale and dimension must consequently be rather meaningless, since the actual geometrical space between objects is changing as
universal expansion continues.
I then discovered the work of Hermann Weyl, whose 1918 theory of spacetime effectively did away with the concept of "scale," an idea that
also seemed to unite the forces of gravity and electromagnetism (Weyl even went so far as to suggest that distances could be "re-gauged"
randomly from one infinitesimal point to another without affecting any physics). Later, while designing, building and experimenting with hydraulic
models as a civil engineer (I taught physics but never made it as
a real physicist) I learned about dimensional similitude, which relates the properties of scale models in a hydraulic laboratory to their full-scale
constructed versions. Dimensional similitude also teaches us that if you scale up an ant to the size of one of those creatures in the 1954 movie Them!,
the ant's own weight would crush its legs and exoskeleton because structural strength doesn't scale up in proportion to size (by the same argument, Godzilla and King Kong
will always remain purely fictional creatures).

More ants. (Badly-pasted graphic courtesy of Particle Physics: A Los Alamos Primer, Cambridge University Press, 1988)
So it would appear that scale does matter, at least in some contexts. But the idea of scale invariance (or its near cousins gauge invariance, phase
invariance and conformal invariance) in physics and cosmology stuck with me, and its appeal seems to have infected quite a few people since
Weyl established the concept in the early part of the last century.
And speaking of the last century, here's a great article from last November by Wupperthal University's
Erhard Scholz, Professor of Mathematical History and Natural
Sciences (retired) on the influence that Weyl's scale ideas had on late 20th century physics. In the paper, Scholz, who has studied and written extensively on
Weyl's mathematics and physics (Weyl's physics is understandable, but his math for me remains impenetrable), summarizes how Weyl's ideas experienced a
comeback in the 1960s (Brans-Dicke scalar tensor theory) and a renewal of interest with such notable luminaries as Dirac, Schild, Bohm and Smolin, who
have all
addressed various aspects of Weyl's geometry. (Scholz' paper is long but very readable, with little mathematics.)
On a side note, Scholz also describes the conformal (but purely non-Weylian) gravity work of Mannheim and Kazanas,
whose fascinating research nevertheless is based on Weyl's conformal tensor \(C_{\mu\nu\alpha\beta}\) (you can download a copy of
M&K's seminal paper from my July 16, 2011 posting). These researchers rightly believe that the Weyl conformal tensor may hold the key to the mystery of
dark energy.
Lastly, I will mention the work of Oxford's
Roger Penrose, whose
Weyl curvature hypothesis attempts to explain what might have been
going on when the Big Bang occurred and what might be the ultimate fate of the universe. Penrose posits the possibility that in the far distant future, when all matter has been devoured
by black holes and the black holes have evaporated via Hawking radiation, the universe will find itself consisting of nothing but stray, high-entropy photons.
The concept of scale, distance, velocity and even time will then have no meaning, at which point the universe will "reset" itself into a low-entropy state
and initiate another Big Bang via a quantum fluctuation (or God, or whatever).
And off we go again! To this day, Weyl's theory astounds all in the depth of its ideas, its mathematical
simplicity, and the elegance of its realization. The basic features of
the program of unified geometrized field theories are especially clearly manifested
in it.
— Vladimir Vizgin, Unified Field Theories in the First Third of the 20th Century
|
| Does the Cosmos Create? (Spoiler Alert) — Posted on Friday, December 7 2012
|
Theories permit consciousness to jump over its own shadow, to leave behind the given, to represent the transcendent, yet,
as is self-evident, only in symbols. — Hermann Weyl I picked up Howard Bloom's latest book
The God Problem: How a Godless Cosmos Creates last night from my local library and was up til midnight reading its 600 pages. By the time I finished I regretted
having wasted the effort — I
still do not know how a godless cosmos creates anything, or why, and neither does Mr. Bloom.
The above lesser-known quote by Hermann Weyl decorates the lead-in to Chapter 8, "The Amazing Repetition Machine" but it really has nothing to do with anything in
that chapter other than provide the fact that Weyl taught the noted information theorist Claude Shannon. However, the book does focus a lot of effort on the notion
that mankind's hugely successful forays into mathematics and physics have led to the recognition that the universe reveals itself through patterns,
which themselves result from the repetition and iteration of simple rules. Indeed, that is Bloom's basic thesis: that the cosmos creates its seemingly
godlike complexification through dogged adherence to simple rules and laws.
If you're like me you will not like Bloom's Five Heresies, which he trots out early on as the basic tools needed to solve the God Problem. They are:
- A does not equal A, and \(x\) does not equal \(x\)
- One plus one does not equal two
- The second law of thermodynamics is wrong
- Randomness is a mistaken notion
- Information is not information
(Animal Farm, anyone?) Bloom tells lengthy stories to support each of these statements, and I have to admit that they're pretty interesting in themselves, if not convincing. For example,
he explores the old tale of a ship that sets out on a lengthy voyage carrying lumber to replace and repair waterlogged and damaged planks and such, and by the
time it arrives at its destination there are two ships, one consisting of an identical, new ship towing the old one, which has been constructed from the
refurbished old parts. The question is: If both ships are identical to the one that set out, which is the original ship? Bloom's take on this, which I agree with,
is that if identical twins, be they ships or human beings or protons or quarks, have experienced different histories, then they cannot
be considered truly identical. Thus, A does not equal A, although it's a useful approximation to think so.
If you're familiar with Einstein's theories and the work of Newton, Leibniz, Riemann, Shannon, Mandelbrot, Wolfram and numerous other scientific and mathematical luminaries
then you can skim through much of the book's wordy expositions without missing anything. The toughest part of the book is actually Chapter 1, in which Bloom
teases (rather, annoys) the reader with seemingly unending lead-ins to what the God Problem is gonna teach
you
(the GP will do this, the GP will do that, ad nauseam). In the end it does nothing but pose the same ancient question: If there is no God, how
did all this complicated stuff come about?
To me the book is a bit like the ol
d rock songs Light My Fire and House of the Rising Sun — they're good songs, they're
worth listening to and all, but the musicians knew they had a good thing so they went overboard on the songs' durations. (In the 1960s, the old rock stations routinely
clipped the long keyboard portion of LMF.) In short, the book is just too damned long.
Example? While asserting that "the computer is the ultimate repeater," Bloom's book is full of unnecessary redundancies, like this paragraph:There is also a chance that
we have free will, competition, dominance heirarchies, love, and war because they are among the earliest outgrowths of attraction and repulsion, among the first manifestations of
differentiation and integration. There is also a good chance that we have free will, competition, dominance heirarchies, love, and war because they are outgrowths of the
starting rules of the universe. Or, to put it differently, there is a good chance that we have free will, competition, dominance heirarchies, love, and war because they are
among the earliest iterations of the axioms that big banged this cosmos. (Thank God for cut and paste.)
The book's saving grace is that it will introduce many readers to the work of Stephen Wolfram, the boy genius (PhD in physics at age 20 from Caltech and
developer of the Mathematica computer algebra system) who turned from quantum physics to the study of algebraic cellular automata in a quest to understand how the
universe works at its base level. His massive, 1,200-page book
A New Kind of Science (2002) explores how exceedingly complicated systems can arise from a few simple, almost trivial mathematical rules (rather like Mandelbrot's fractals).
I bought the book when it came out and was amazed at the many (many!) pretty computer graphics, but I donated the book to my public library as it was just too much for me to absorb.
(The Pasadena Library now has three copies of this book, so there must be other intellectual sluggards like me in town.)
To summarize, if you're wondering what science has to say about how the universe might possibly exist without a god, then read this book and educate yourself to how many scientists
have addressed that same question.
Bloom has made a notable attempt in his book to show that the universe can get along quite well without a god, but in doing so he gives the cosmos a mind of its own, which
to me is no different than a god. Along the way he tells some pretty interesting stories about how modern mathematics came about and how scientific theories have enabled us
to meaningfully address that very important question.
|
| Big — Posted on Tuesday, November 28 2012
|
|
I'm posting this mainly as an excuse to put up this neat photo, the exact center of which contains an interesting object:

Astronomers at the University of Texas at Austin's
McDonald Observatory
have discovered the most massive black hole to date. Located in the spiral galaxy
NGC 1277 in the Perseus Constellation, the hole has a mass that is approximately 17 billion times that of our Sun, while its event horizon exceeds the diameter of the planet
Neptune's orbit by a factor of 11. But falling into this black hole from the event horizon would seem uneventful (no pun intended) — tidal forces would probably not
even be detectable, and the
observer would have plenty of time (about two weeks) to think about her fate before she is absorbed into the central singularity.
The NGC 1277 black hole, which accounts for some 14% of the total mass of its entire host galaxy, is significant because t
he mass of a typical black hole constitutes
less than 0.1% the mass of their
surrounding galaxies. The discovery also punches a hole in recent theories relating the evolution and rotation rate of galactic stars with the mass of their central black holes.
Ever wonder what it would be like inside the event horizon of a black hole? This might give you an idea:
There's at least an Avogadro's number (10\(^{23}\)) of stars in the observable universe and, if we assume that each star has about the same mass on average as
our Sun (10\(^{30}\) kg), then the total mass M of the universe would be roughly 10\(^{53}\) kg. The radius of the event horizon for such a mass is given by \(R = 2GM/c^2\), which
comes out to about 10\(^{26}\) meters, or roughly 10\(^{10}\) (10 billion) light-years. This is within an order of magnitude of the known radius of the universe, though
it's on the short side, so it's unlikely that we're residing in a black hole.
However, I've neglected the mass (or mass-energy) of all the planets, asteroids, nebulae, gas, neutrinos, photons and dark matter/dark energy in the universe, so it's
still possible that
we're living within
the event horizon of a gigantic black hole. If that is the case, then you already know what it's like inside the horizon.
But you might also be wondering what's on the outside of all this. I've wondered about that, too. Let me know when you have the answer.
|
| Pixie Dust Science — Posted on Saturday, November 24 2012
|
Marco Rubio,
the junior US Senator from Florida and presumed 2016 GOP presidential candidate, was recently asked what he believed was the
age of the Earth. "I'm not a scientist, man" was his measured response, although Rubio made it clear that the idea of a 5,000-year-old Earth as
claimed by religious fundamentalists is just as valid as any other estimate based on scientific inquiry, and should be studied in America's
schools. I'm totally with NY Times columnist and Nobel economics winner
Paul Krugman on this topic, as he
bewails the intentional ignorance of the recently chastised (but unrepentant) Republican party when it comes to non-scientific dogmatic belief.
But a
s the issue involves time (a favorite subject of mine), I thought it appropriate to address it within a Weylian context. So bear with me.
As anyone who has followed this site knows, in 1918 Hermann Weyl proposed a brilliant theory that appeared to unify gravitation and electromagnetism,
the only two forces known at the time, within a single geometric framework.
The theory relied on a simple generalization of Riemannian geometry, which itself assumes the invariance of vector magnitude or length
under physical transport. By allowing the length of a vector to change from point to point in an electromagnetic field, Weyl was able to derive Maxwell's
equations from a purely geometric basis. His theory also introduced the idea of gauge invariance to physi
cs, which has since become a
cornerstone of modern quantum theory.
However, Weyl's theory was overturned by Einstein, an early admirer of the theory, who pointed out that the magnitude of a vector could also be related to
the ticking of a clock. And while Einstein (who demolished the idea of absolute time with his own 1905 theory of special relativity) in principle had no argument
against the non-invariance of ticking clocks, he did note that there were certain instances where ticking rates should definitely not change. Shortly after
Weyl published his theory, Einstein argued that the spacings of atomic spectral lines (such as the double line of atomic sodium) must themselves be absolute, as they
are never seen to vary either from point to point or from one time to another. Weyl tried to mount an effective counter argument, but Einstein's point was irrefutable
and by 1921 Weyl's theory was all but abandoned.
 \(\leftarrow\) Detail of Einstein's April 1918 postcard to Weyl, outlining E's objection to W's theory
based on the time difference that an arbitrary vector would experience when transported over two differing spacetime paths. In Weyl's theory, the rate of a ticking
clock, as well as the total time difference, depends on the vector's past history. \(\leftarrow\) Detail of Einstein's April 1918 postcard to Weyl, outlining E's objection to W's theory
based on the time difference that an arbitrary vector would experience when transported over two differing spacetime paths. In Weyl's theory, the rate of a ticking
clock, as well as the total time difference, depends on the vector's past history.
But there is another version of the invariant ticking clock, and that is the decay rate of radioactive isotopes. We are taught early on in university that the half-life of
an unstable isotope is fixed and immutable, the rate of decay being a property of the weak force of quantum mechanics. For example, while the decay of any given atom of
\(^{226}\)Ra cannot be predicted to occur with any accuracy, it is well known that a sample of radioactive radium containing many trillions of atoms will decay at a very
precise rate over time — in 1,601 years almost exactly half of the sample will have decayed to Radon-222 via alpha decay. The slight imprecision in the rate of
decay is due primari
ly to observational limitations and uncertainties, although there are examples in which the imprecision is much higher. It may be surprising to learn that
the ordinary neutron, while completely stable within the nucleus of an atom, is in fact unstable. A collection of free neutrons will decay to protons, electrons and
antineutrinos in 10 to 15 minutes. (It is somewhat difficult to assemble an Avogadro number of neutrons for decay-measurement purposes!)
It may also be surprising to learn that not every physicist is an adherent of the immutability of isotope decay, and this has led recently to renewed attacks by
fundamentalist Christians on the presumed 4.5-billion-year age of the Earth, a figure that has been determined almost solely through radioisotope decay rates.
Before the advent of radiometric dating, fundamentalists could always rely on screwy, implausible reasoning to explain away fossil evidence (God placed them in the
ground to test our faith, or Satan put them there to deceive us) or slightly plausible rationalizations based partly on scientific fact (radiocarbon dating is wrong because
the flux of solar radiation has varied over the past 50,000 years).
But, faced today with seemingly insurmountable physical, biological, geologic and radiometric data, fundamentalists
have happened upon the "accelerated decay" theory, which states that when the Earth and mankind were formed by God 5,000 years ago the rates of
radioisotope decay were billions of times faster than those measured today, a claim that would explain the apparent extreme age of the Earth.
And recent scientific research on the assumed constancy of radioactive decay is giving them
some ammunition. In 2006 two Purdue University physicists, Jere Jenkins and Ephraim Fischbach, spotted what they believed was a
statistically significant correlation between
the observed decay rate of a micro-Curie sample of Manganese-54 and solar flare activity. Supporting some related research findings, the scientists detected
an apparent decrease in the decay rate of \(^{54}\)Mn with increased neutrino, x-ray and proton fluxes from solar flares. The decrease was tiny (about 0.015%),
but sufficient for at least one
biblical archaeology group to claim that the "smoking gun" of accelerated decay had been found.
Other
research
has focused on the possible effect of changes in the Earth's magnetic field and the Sun-to-Earth distance on radioisotope decay rates, with each study
reporting a possible correlation.
One study
has even reported that decay rates can be dramatically increased by encasing radioactive materials
in metal cylinders and lowering the materials to extremely low temperatures, giving rise to the hope that dangerous radioactive wastes from nuclear
power plants and weapons manufacturing could be suitably "treated" by reducing the waste containment time from thousands of years to perhaps less than two years.
But the majority of such studies have shown no such changes in decay rates, and it remains highly probable that isotopic decay is indeed a fixed constant for
every radioisotope under all anticipated environmental conditions. This will not allay the fundamentalists, however, who can always claim that "something
happened" in biblical times that explains it all away in favor of a 5,000-year-old creation event.
Finally, I return to Weyl. Is it possible that his theory can be amended to allow for fixed clock rates under physical transplantation, thus upending Einstein's
objection of the theory?
The question is of far greater importance than might be imagined, although you have to be a total nerd to appreciate its importance. Suffice it to say that
many physicists and mathematicians have addressed the problem, including the great Paul Dirac on one end and lowly me on the other. It has nothing to
do with Einstein's relativity theory, time dilation and the Lorentz-Fitzgerald contraction, all of which are perfectly understood and accepted, but
instead involves the nature of time at the microscopic level. Weyl suggested that what goes on at the atomic level regarding time is a true puzzle, since all
our measurements have to be performed at the macro level. But measurements of things like the spacing of spectral lines and radioisotope decay rates
at least get us close to what is going on at the micro level, although the geometry of spacetime and the nature of time down there remains illusive.
We may never know, but to me it's far better than the dogmatic, fundamentalist magical pixie dust being thrown around to explain things.

|
| Merkelstrasse 3 — Posted on Thursday, July 26 2012
|
 Here's an odd little
YouTube video showing that Herm
ann Weyl and his family lived at
Merkelstrasse 3 from 1930 to 1933 in Göttingen, Germany. Weyl reluctantly accepted the chair of the mathematics department when the previous chair,
David Hilbert (Weyl's mentor and PhD advisor from 1904 to 1908) took mandatory retirement in 1930. Hitler's ascension to the chancellorship
of Germany in January 1933 was the rea
son Weyl and his family left that year, along with Einstein and many other Jewish scientists, professors, teachers and public
service employees (who were all summarily fired by the Nazis in April 1933). Weyl was Christian but his wife Hella was a Jewish intellectual, a situation that
placed their sons Michael and Fritz in jeopardy from the National Socialists. Here's an odd little
YouTube video showing that Herm
ann Weyl and his family lived at
Merkelstrasse 3 from 1930 to 1933 in Göttingen, Germany. Weyl reluctantly accepted the chair of the mathematics department when the previous chair,
David Hilbert (Weyl's mentor and PhD advisor from 1904 to 1908) took mandatory retirement in 1930. Hitler's ascension to the chancellorship
of Germany in January 1933 was the rea
son Weyl and his family left that year, along with Einstein and many other Jewish scientists, professors, teachers and public
service employees (who were all summarily fired by the Nazis in April 1933). Weyl was Christian but his wife Hella was a Jewish intellectual, a situation that
placed their sons Michael and Fritz in jeopardy from the National Socialists.
The Merkelstrasse address now appears to be an editorial publishing house for an experimental psychology magazine!

Built in 1907, it appears to be a beautifully preserved building.
|
| Weyl and String Theory — Posted on Sunday, July 1 2012
|
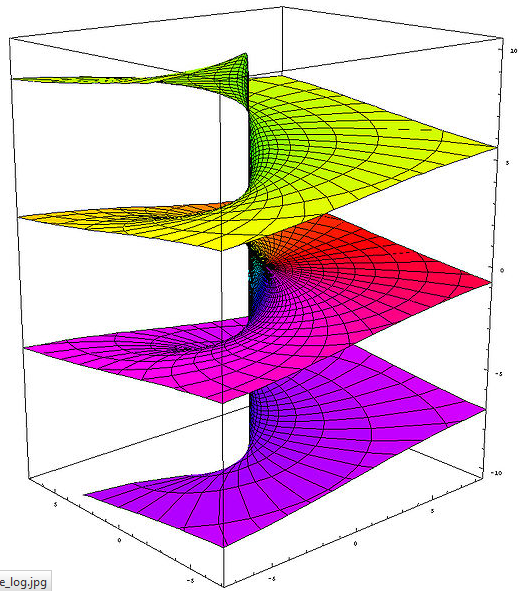 Published in 1913 when the author was only 27, Hermann Weyl's first book was titled The Concept of a Riemann Surface
(you can download it legally for free
here, although it's in German). I won't bore you with the details (which I barely understand anyway),
but a Riemann surface is basically one or more "sheets" in the complex plane described by \(z = x + iy\) or \( z = r \exp(i\theta) \). A multivalued function such as \(\log(z) \) traces out
an infinite number of such sheets, resulting in a winding surface resembling a screw with wide, thin threads like that shown. So what does this have to do with string theory?
Published in 1913 when the author was only 27, Hermann Weyl's first book was titled The Concept of a Riemann Surface
(you can download it legally for free
here, although it's in German). I won't bore you with the details (which I barely understand anyway),
but a Riemann surface is basically one or more "sheets" in the complex plane described by \(z = x + iy\) or \( z = r \exp(i\theta) \). A multivalued function such as \(\log(z) \) traces out
an infinite number of such sheets, resulting in a winding surface resembling a screw with wide, thin threads like that shown. So what does this have to do with string theory?
In one of Leonard Susskind's YouTube lectures on the theory (see my June 14 post), you'll notice that at one point he seems to go off on a tangent, talking about the complex plane, the
Cauchy-Riemann conditions and conformal mapping. But then he shows how all this relates to interacting strings. I thought it was all rather abstract, and felt that Susskind's approach
couldn't really have anything to do with reality. But then I went back to a long-neglected book that has sat on my shelf for too long to find out just what the hell Susskind
was talking about.
While my understanding of the subject is still pathetic, I finally finished reading Barton Zwiebach's
A First Course in String Theory
(2004) and can now claim a Kindergartener's grasp of what the theory is all about. And the book also conveniently explains what Susskind was talking about
(although, by comparison, to me Susskind's treatment is akin to nursery-level physics compared with Zwiebach's).
Zwiebach's book stands as a godsend for semi-conscious people like me, but it still has its pro
blems. One concerns the author's teasing the reader with one damned string lagrangian
after another until, at last, in Chapter 21, we get to the Polyakov lagrangian, which is the one the reader has waded patiently through some 462 pages to get.
But it's worth it. For one thing, you discover that the world-sheets of strings (at least open strings) are Riemann surfaces. More interestingly, these sheets are invariant to
Weyl transformations, meaning the lagrangian does not change when the sheet metric is multiplied by an arbitrary function of the string coordinates (such transformations
are also called conformal). Consequently, the concept of distance on the world-sheet becomes meaningless. To me, all of this has a familiar ring to it.
While it's probably nothing more than an example of the wonderful consistency that mathematics displays throughout physics, I immediately saw an analogy of the string approach with
several of Weyl's theories. For one, Weyl's conformal lagrangian \(\sqrt{-g}\,C_{\mu\nu\alpha\beta} C^{\mu\nu\alpha\beta}\) (which may have relevance to the
cosmological problem of dark matter) is also invariant with respect to the metric transformation
\(g_{\mu\nu} \rightarrow \lambda(x)^2 g_{\mu\nu}\); here too, the concept of distance becomes meaningless. Similarly, in Weyl's 1918 theory (in which he attempted to unite electrodynamics
with gravitation), distance scales lose all relevance as well.
Although it would be preposterous to think that Weyl's work on Riemann surfaces, non-Riemannian geometry and cosmology has anything to do with string theory, I believe Weyl would
have accepted
string theory with enthusiasm if only in view of the possibility that the theory successfully unites gravity with electromagnetism and quantum mechanics, a topic that was always of much interest to him.
And, given the fact that the theory involves strings that will
almost certainly never be detected (they're on the order of the Planck length in size) and energies that will likely never be attained in any accelerator, Weyl would probably have delighted
in musing over the philosophical (and perhaps religious) aspects of string theory as well.
PS: I have Zwiebach's first edition book, but he published a second edition in 2009
that includes a lot more material. At nearly 700 pages, it's 150 more than the first edition and includes
more advanced topics like superstrings. I'd like to read it, but oh, my aching brain.
|
| Turing at 100 — Posted on Saturday, June 23 2012
|
|
Over a hundred years ago, the famous German mathematician David Hilbert (and Hermann Weyl's PhD advisor) declared that rigorous logic would
one day solve all mathematical problems, including Fermat's last theorem and Riemann's hypothesis, perhaps the two most vexing problems of Hilbert's day. Then,
in 1931, Kurt Gödel published his famous treatise on incompleteness, which effectively proved that there are problems that mathematics and logic will
never be able to solve.
Today is the 100th birthday of the British mathematical logician Alan Turing (which is
why the above panel from today's Google's search page looks the way it does). You can read about Turing's brilliant
though tragic life
elsewhere, but here I will only point out that in 1936 Turing provided a superior proof of Gödel's incompleteness theorem
s, while at the same time inventing what is today
known as the Turing machine. You can read about this interesting chapter in Turing's life (which preceded his famous decryption work at Bletchley Park) in
Gregory J. Chaitin's 2007 book
Thinking About Gödel and Turing: Essays on Complexity, 1970-2007. As for the hypothetical
Turing machine, I never knew any more about it
other than it provided the basic plan for modern co
mputers and that, by refusing to halt when programmed for certain simple problems, essentially proved Gödel's incompleteness
theorems.
As described in the book, many notable mathematicians—Weyl and John von Neumann, in particular—were dazed and even somewhat troubled
by the discoveries of Gödel and Turing. In 1942
Weyl remarkedWe are less certain than ever about the ultimate foundations
of [logic and] mathematics. Like everybody and everything in
the world today, we have our "crisis" ... Outwardly it does not seem to hamper our daily work,
and yet I for one confess that it has had a considerable practical
influence on my mathematical life: it directed my interests
to fields I considered relatively "sa
fe," and has been a constant
drain on the enthusiasm and determination with which I pursued
my research work. This experience is probably shared by other
mathematicians who are not indifferent to what their scientific
endeavors mean in the context of man's whole caring and knowing,
suffering and creative existence in the world. Turing's suicide nearly 60 years ago, brought about by imposed chemical castration mandated by a prudish British government's
discomfort over the man's sexual preferences, brought to an end a brilliant career just when major progress in electronic computing was beginning to yield results. It is not inconceivable
that, had he lived, Turing himself would have owned a MacBook Pro and even participated in the development of computer algebra programs like Mathematica.
One last story regarding Turing — In May 1942, Paul Dirac (who I consider the most brilliant physicist who ever lived) was appr
oached with an offer to work at Bletchley Park with Turing and fellow
mathematical genius Max Newman. But as it would have meant leaving his pregnant wife Manci behind, Dirac had to turn it down. Dirac as a cryptologist—that would have
been interesting!
|
| Intuitive v. Analytical — Posted on F
riday, June 22 2012
|
As Albert Einstein once said to me: "Two things are infinite: the universe and human stupidity." But what is much more widespread than the actual stupidity is playing
stupid, turning off your ear, not listening, not seeing. — Friedrich S. Perls, Gestalt pioneer Years ago a friend of mine and I had a discussion about faith
with his devoutly Christian mother.
She related a story about his father, who survived a mortar attack in the Korean War. It was the standard "there are no atheists in foxholes" argument, and
my friend and I knew it all too well. "Soldiers live and die in wars, and God has nothing to do with it," he replied. She countered with "Yes, but when you're being shot at it's nice
to know someone's looking out for you." My friend and I were both struck by the obvious stupidity of this circular argument, but we let it drop there.
The July issue of Scientific American has an editorial piece on
System 1 thinking (which is the gut-level, intuitive type of mental response to an issue or problem) and System 2 thinking (which is
more analytical and nuanced, requiring consideration and thought), and how these types of thinking might be related to the belief in God. The
article points to recent
research that supports the notion that System 1 thinkers
tend to be more religious, while System 2 thinkers tend to be agnostics or atheists.
Even a casual glance at any FOX News show will tell you the type of thinking it encourages. When questions like "Do you believe the United States should torture terrorist suspects?"
are posed, you'll typically hear an immediate "Yes!" By comparison, MSNBC tends to encourage more weighted consideration of such questions by its reporters. Overall, conservatives generally
tend toward quick, gut-level opinions of issues, while liberals are generally more nuanced and analytical. Behavioral psychologists have now confirmed this notion.
But Jessica Griggs of
New Scientist writes that
modern scientific theories like quantum mechanics are inherently non-intuitive and serve to dispel the notion that the world is understandable at the gut level.
To demonstrate this, she points to a
new paper by Esther
Hänggi and Stephanie Wehner of the Centre for Quantum Technologies at the University of Singapore that demonstrates convincingly
that a violation of
Heisenberg's Uncertainty Principle would necessarily violate the Second Law of Thermodynamics—it doesn't get much more non-intuitive than that! (I've provided a simple
derivation of the Uncertainty Principle in my May 3, 2011 posting.)
Griggs explains this assertion by using a clever appeal to basic thermodynamics
via information theory: Fit a small piston to a container of gas at some finite temperature. By violating the Uncertainty Principle, you could obtain additional information about the
momentum and position of the gas molecules beyond that which you would otherwise have no access to. Then, by monitoring the motion of the gas particles nearest the piston head,
you could adjust the orientation of the piston so that only those molecules directed toward the piston would be allowed to strike it. You could therefore extract useful work from the
container, effectively lowering the internal heat energy of the gas, regardless of its temperature. This is a direct violation of the Second Law.
How does one resolve this? System 1 thinkers might be tempted to say that the Second Law and the Uncertainty Principle are "just theories" and can therefore be violated
using clever technological tricks and go-arounds. But this would mean that perpetual motion machines (called "impossible machines" by Hänggi and Wehner) can be built. And why
haven't they been built? Again, System 1 thinkers would say that no-one has yet been clever enough to construct one. The appeal of this kind of thinking is obvious—it doesn't
require any effort! Pity the poor System 2 thinker: she goes out and gets educated, then struggles for 5 to 6 years getting a PhD, only to discover that it's System 1 thinking that rules the
world. It would seem that while knowledge is power, ignorance is even more powerful.
The only meaningful advantage we humans have over other forms of life on this planet is the ability to reason. Our nearest genetic cousins, the apes, will never be able to understand or
appreciate the amazing mathematical, technological and intellectual discoveries their so-called betters have achieved. Yet many of us refuse to accept the truths that scientists have struggled
so hard to secure since we left the trees and savannas. I would argue that those people—the System 1 thinkers who believe that information and knowledge are dangerous or at least not
worth the effort—are no better than apes.
|
| Susskind on String Theory — Posted on Thursday, June 14 2012
|
 Leonard Susskind, the Felix Bloch Professor
of Physics at Stanford University, is one of the fathers of
string theory. Born to a poor Jewish family in the Bronx in 1940, he started out life as a plumber to help out his ailing father. The story goes that when he
told his father he wanted to be
an engineer, he was told "Hell no, you ain't gonna drive no train!" When Susskind decided later that he wanted to be a physicist, his father replied "Hell no, you ain't gonna work in
no drug store!" Another story tells about his being stuck in an elevator in 1968 with Caltech's Nobel Laureate Murray Gell-Mann. When asked idly what he was working on, Susskind
replied that he was studying the possibility that particles may actually be tiny Planck-sized strings, at which point Gell-Mann laughed riotously at such a silly idea. Leonard Susskind, the Felix Bloch Professor
of Physics at Stanford University, is one of the fathers of
string theory. Born to a poor Jewish family in the Bronx in 1940, he started out life as a plumber to help out his ailing father. The story goes that when he
told his father he wanted to be
an engineer, he was told "Hell no, you ain't gonna drive no train!" When Susskind decided later that he wanted to be a physicist, his father replied "Hell no, you ain't gonna work in
no drug store!" Another story tells about his being stuck in an elevator in 1968 with Caltech's Nobel Laureate Murray Gell-Mann. When asked idly what he was working on, Susskind
replied that he was studying the possibility that particles may actually be tiny Planck-sized strings, at which point Gell-Mann laughed riotously at such a silly idea.
A number of years ago I bought A First Course in String Theory by MIT's Barton Zwiebach. Overjoyed at the thought of finally learning this difficult subject at
a fairly decent mathmatical level,
I was quickly dismayed to find that, halfway through the book, I was hopelessly lost in the material. I've since fared
no better with other books at a similar
level, while books such as String Theory for Dummies were so simple that I may as well have been learning it from Readers Digest.
Fortunately, Susskind also has a true gift for teaching, which comes in handy for people (like me) who thought that string theory was unlearnable. Susskind has posted many dozens of his lectures
on YouTube, on subjects ranging from classical physics to quantum cosmology, but it was only recently that he starting posting lectures on string theory and M-theory. The best
is a ten-part, 17-hour lecture series that begins with Lecture 1. By the end of the entire series I can practically
guarantee that you will understand the basic mathematics of string theory, and much more. For example, in Lecture 5 you learn the neat fact that
$$
\frac{1}{2} \sum_{n=1}^\infty n = \infty - \frac{1}{24} $$
and how this is tied to the requirement that bosonic string theory needs 26 dimensions to make sense. (That is, 24 space dimensions plus the boost and time. Susskind jokingly
suggests that it's 26 also because you run out of letters in the English alphabet at that point.)
While not what you would call the absent-minded professor type, Susskind nevertheless often displays the archetypal bumbling scientist who occasionally forgets factors of 2 and such and has
to be reminded by
the students in his class about simple matters like plus and minus signs (and his pronunciation of "Noether" is also quite endearing). Furthermore he is very fond of cookies,
which he munches on constantly during his lectures (he seems to be in pretty good shape, but at 72 he should really watch this).
Susskind is also very patient with the occasional knucklehead who interrupts him to ask stupid questions (I wish they would edit out these interruptions from the videos,
which tend to be annoying).
An incomplete set of class notes can be found here.
Overall his lectures are just plain informative fun. Whenever I get tired of listening to music on my iPod while jogging or working out in the gym, I put Susskind on.
|
| Then He Was Gone -- Posted on Saturday, June 2 2012
|

After his retirement from the Institute for Advanced Study in Princeton in 1952, Herman Weyl and his wife divided their time between Princeton and Zürich. On the occasion of Weyl's
70th birthday on November 9, 1955, IAS Director J. Robert Oppenheimer cabled the Institute's best wishes to Weyl in Switzerland. Weyl wrote back to Oppenheimer on November 27,
thanking him and expressing his gratitude
for his acceptance into the Institute in the eventful year of 1933.
Eleven days later Weyl died in Zürich from a massive heart attack.
Here is the letter. I find it amusing that Weyl's English, while very good, still shows grammatical traces of his native German.
Posting courtesy of The Shelby White and Leon Levy Archives Center, Institute for Advanced Study, Princeton, New Jersey. The Weyl letter file is
copyrighted material; please comply with the Institute's rules regarding its use.
|
| Weyl's Wormhole and Other Neat Stuff -- Posted on Tuesday, May 29 2012
|
 Sorry for this long post. I adapted it from a high school article I wrote in 2008. Sorry for this long post. I adapted it from a high school article I wrote in 2008.
Columbia University's Brian Greene has a 4-page
article in the May 28 edition of Newsweek that, while not exactly new material, provides one of the better popular descriptions of the multiverse concept. The multiverse is a (very) hypothetical idea in which our universe is just one of many (possibly infinite) universes, each having its own set of physical constants (I used to view Christ's comment about "many mansions" as a hint about the multiverse, but He probably wasn't aware of it). And the issue as to how we might actually travel to another universe is (and may always be) totally unanswerable.
Shortly before his death from injuries sustained at the front in World War I, in 1916 German physicist Karl Schwarzschild solved Einstein's gravitational field equations for the simplest possible case, a spherically symmetric space with a central point mass. His discovery, which came just months after Einstein announced his theory in late November 1915, is the basis for the gravitational deflection of light (confirmed in 1919), the explanation for the advance of perihelion of the planet Mercury (derived by Einstein in 1917), and the gravitational redshift of light. It also provided the simplest description of a non-rotating black hole, although this fact was not appreciated until many years later. The Schwarzschild solution is described via the metric
$$ ds^2 = (1 - 2m/r) \, c^2 dt^2 - \frac{1}{1-2m/r} \, dr^2 - r^2 (d\theta^2 + \sin^2 \theta \, d\varphi^2) $$
where \(m\) is the geometric mass of the central gravitating object of mass \(M\) (\(m = GM/c^2\)) while \(r, \theta, \varphi \) are the usual polar coordinates, and \(ct \) is the time coordinate.
Obviously, at the so-called Schwarzschild radius or event horizon (\(r = 2m\)) the radial coefficient becomes infinite. If the mass \(M\) is contained completely within this radius, then you have a black hole. This is believed to occur when stars run out of nuclear fuel and collapse upon themselves; gravity becomes so powerful that no known force stop the collapse, and the object shrinks to a mathematical point having mass \(M\) and infinite density.
It can be shown that a distant observer watching the infall of an object would see the object appear to slow down and redshift as it nears the event horizon. At a small distance from the horizon the object would seem to stop completely, although it would also be redshifted to the point of invisibility. So how could anything actually fall into a black hole if it takes an infinite amount of time, and for that matter how could a black hole even form in the first place?
But the Schwarzschild metric has an even bigger problem, which was spotted not long after its announcement. Consider a light ray falling onto the mass along some fixed \(\theta\) and \(\varphi\). Then \(ds^2 = 0\), so that the radial velocity of the light ray is
$$ \frac{dr}{dt} = c \, (1 - \frac{2m}{r}) $$
At the event horizon the velocity of light falls to zero, apparently violating one of the two principle tenets of Einstein's special relativity.
But not to worry, as all these problems can be traced to the Schwarzschild metric's coordinate system itself. The main thing about relativity is that any coordinate system is as good as any other, and Schwarzschild's use of the familiar coordinates of spherical geometry betray an all too-human tendency to think that the world must conform to our idea of what's most comfortable or familiar.
In 1917, Hermann Weyl was also thinking along these lines. He came up with a new coordinate \(\rho\) that replaced Schwarzschild's \(r\) to create what is today known as isotropic coordinates (kind of a misnomer because only the \(r\) coordinate is changed). In Weyl's isotropic coordinate system, Schwarzschild's metric becomes
$$ ds^2 = \frac{(1 - m/2\rho)^2 }{(1 + m/2\rho)^2 }\, c^2 dt^2 - (1 + m/2\rho)^4 \, (d\rho^2 + \rho^2 \, d\theta^2 + \rho^2 \, \sin^2 \theta \, d\varphi^2) $$
(Weyl's isotropic coordinate is very easy to compute; even a high school calculus student can do it.) There is now no funny behavior at \(\rho = 2m\) (though the time coefficient shrinks to zero at that point), and both coefficients remain positive until the radius goes to zero, where both coefficients blow up. Unfortunately, the velocity of light during radial infall still goes to zero in isotropic coordinates.
Over the next few years Einstein, Eddington and others also tried their hands at different coordinate systems for the Schwarzschild metric. It seems remarkable today that, within three or four years of Einstein's unveiling of the general theory or relativity, so much progress was made in investigating this metric. However, the solution that eluded them all was the one that would leave the velocity of light a constant. It was simplicity itself to
write it down:
$$ ds^2 = F(\bar{r},\bar{t}) [c^2 d\bar{t}^2 - d\bar{r}^2 ] - r^2(d\theta^2 + \sin^2 \theta \, d\varphi^2) $$
where \(F\) is some function (without zeroes) to be determined and \(\bar{r}, \bar{t} \) are new coordinates replacing \(r\) and \(t\) (most references call the new coordinates \(u\) and \(v\)).
For a light ray we then have
$$ \frac{d\bar{r}}{d\bar{t}} = c $$
everywhere. But finding the coordinate transformation that would provide this was devilishly difficult, and it wasn't discovered until 1960, when Martin Kruskal submitted his now-famous
paper on the problem. While solving the constancy-of-light-velocity problem, it also provided a bonus — the possibility that the transformed Schwarzschild metric was a fiendishly disguised description of a wormhole.
It is said that Hermann Weyl was the first person to suggest the possibility of wormholes, although the 1921 paper he wrote on the subject mainly dealt with the motion of two bodies in an axially-symmetric Schwarzschild metric.
The so-called Kruskal-Szekeres metric (Szekeres discovered it independently, also in 1960) are given by the goofy-looking set of expressions
$$ c \bar{t} = \frac{1}{2} |2R-1|^{1/2} e^R [e^T - \frac{|2R-1|}{2R-1} e^{-T}] $$
$$ \bar{r} = \frac{1}{2} |2R-1|^{1/2} e^R [e^T + \frac{|2R-1|}{2R-1} e^{-T}] $$
$$ F(\bar{r}, \bar{t}) = \frac{8 m^2}{R} \, e^{-2R} $$
where \(R = r/4m \) and \(T = ct/4m \) (note that the bracketed terms with \(e^T \) and \(e^{-T}\) can be either \(\sinh T\) or \(\cosh T\) depending on the sign of \(2R - 1\)).
The Kruskal-Szereres metric holds all the way down to \(r = 0\) and then some. It in fact describes two branches of an infinite set of hyperbolas (with \(\bar{r}\)
and \(c\bar{t}\) acting as the \(x\) and \(y\) coordinates); the "throat" between the branches can be viewed as a wormhole to the past and future. Unfortunately, subsequent investigation has shown that nothing can actually traverse the wormhole unless the traversing object is made of some kind of exotic (negative) matter (although this hasn't stopped science fiction writers from using wormholes in their stories). The singularity at
\(r = 0\) actually represents the hyperbola \( c^2 \bar{t}^2 = \bar{r}^2 + 1 \); space-time would seem to have no meaning above and below the upper and lower branches of the hyperbola.
So did Weyl actually originate the concept of a wormhole? Perhaps he did, but I really doubt that in 1921 he actually considered it as any kind of gateway to other places, times or — as Brian Greene might
suggest — other universes.
Here are two good references on the above material. The graphics in the Collas-Klein paper are particularly helpful in visualizing the Kruskal-Szekeres coordinate system:
Nikodem Poplawski,
Radial motion into an Einstein-Rosen bridge (2010)
Peter Collas and David Klein,
Embeddings and time evolution of the Schwarzschild wormhole (2011)
|
| Absolute Security -- Posted on Sunday, May 27 2012
|
In pursuit of a guaranteed security that not even the richest and most militarily powerful country in human history can realistically
hope to attain, we have been allowing our national institutions to be transformed for the purposes of endless war and empire, gravely endangering the future of our democracy.
... We have allowed ourselves to be seduced by sound-bite formulas that reflect neither our real security needs, nor our constitutional principles, nor our national purposes ... Americans have been sent off on quixotic
preventive campaigns to suppress all present and potential dangers, and they have been warned of the dire consequences of settling for anything less. — David C. Unger,
The Emergency State
First, to set this up, a story. I worked as
a civil engineer (primarily water resources, hydraulic modeling, distribution, treatment and quality) for much of my working life, and when massive zones of groundwater contamination were discovered in
Southern California in the mid-1980s I found myself making public presentations to schools, civic groups and environmental organizations concerned about drinking water quality. Then, as today, water quality involved
primarily pollution prevention, followed by treatment. There are many options available for ordinary water treatment (suspended solids removal, disinfection, etc.), but the removal of synthetic organic pollutants (like the trichloroethylene found in many groundwater aquifers today) generally requires aeration along with advanced methods such as activated carbon adsorption, microfiltration and reverse osmosis. Treatment
efficiency is
dependent on many factors, but
it is generally expressed by a parameter known as log removal, the "log" referring to base-10 logarithms.
An example will suffice: If treatment removes 90.0% of some contaminant, we say that the treatment provides 1-log removal efficiency. Similarly, 99.0% and 99.9% removal is called 2-log and 3-log removal efficiency,
respectively. It's easy to count the 9's, but when a treatment provides something like 94.7% removal efficiency (1.28 log) then you have to use a formula, which I won't bore you with here.
Invariably in my presentations I would be asked the usual questions, like "How much pollutant is removed by a particular treatment process?" and "Is the water safe to drink if 99% of the contamination is taken out?" But
the most common question was always "Why take any chances? Just remove all of the contaminants!"
At that point I would start talking about adding multiple treatment trains in series, or increasing the aeration rate or contact residence time, all of which increases treatment costs, but I would always emphasize that 100% removal efficiency is impossible. Even distilling the water (which would be catastrophically expensive for a water utility) would not provide 100% removal. The nearest thing to perfect
treatment—reverse osmosis—is itself very expensive and still not 100% efficient. But the remark "I still don't see why you don't just take everything out" would invariably persist. My mediocre presentation skills not withstanding, it never dawned on me in those days that a lot of people just didn't get it—there's no such thing as absolute security.
And they still don't get it. In David C. Unger's 2012 book
The Emergency State: America's Pursuit of Absolute Security at All Costs,
the author explains how the American "emergency state" arose from signature institutions like the CIA, the Defense Department and the National Security Council, whose national and global game plans seemed to emerge ready-made from America's victories over World War II Axis powers. Unger asserts that these plans were incremental—not sudden—in coming, but that in the span of seven decades our country's constitutional democracy has morphed into a secretive and permanent emergency state. And this morphing has largely escaped the notice of the American people themselves, who are "often the last to know what their government does in their name abroad," and
then "genuinely mystified as to why foreigners seem so 'anti-American' ."
While Unger, in the words of noted reviewer Andrew J. Bacevich "lays bare the pathologies that have disfigured U.S. national security policy over the course of many decades" brilliantly describes how the country, from FDR to Obama, has increasingly diverted trillions from essential domestic needs to programs of near-paranoid military overkill, he does not seem to know precisely what brought all of this about. He compares Pearl Harbor with the events of
9/11, but each of these events resulted in the deaths of only several thousand people, a relative drop in the bucket compared to what many other countries have experienced, so it is not clear what lies in the hearts of the American people that made them so ripe for the unending right-leaning takeover that continues to grip the country.
Unger concludes his excellent book with a 10-point prescription for ending our state of permanent emergency (re-establishing constitutional wartime checks and balances, etc.), but on the whole it's pretty lame. Ultimately, the direction that the country takes is in the hands of the American people, who unfortunately are too distracted by Lady Gaga, American Idol, Facebook/Twitter and similar trash-culture phenomena to take much notice of the fact that their country's democratic principles are literally dissolving away.
|
| Blast from the Past -- Posted on Saturday, May 26 2012
|
 I really have nothing to do today. I really have nothing to do today.
When I was seven years old (1956) my school started giving us poliomyelitis immunizations, more frighteningly known to us kids as polio shots. To prepare us,
we had to watch this cartoon about vaccination. I only saw it once, but I never forgot it. (I have a fantastic long-term memory, but can't remember what I did last week.
It's called old age.) Anyway, maybe my old schoolmates from Northview Elementary in Duarte, California will remember it. And thanks to
Archive.com, we can all see it again.
From that day on, once a year, we'd bring in our parents' signed approval slips and our one-dollar bills and get marched to the nurse's office for the shots.
Bruce, John, Greg, David and I would always try to look nonchalant to impress the girls, but inwardly we were scared to death of those needles.
Many years later the oral vaccine came out, and the needles disappeared.
Disney's Defense Against Invasion (1943) was also a bit of political brainwashing, but I didn't notice it back then. All I remember is the
cartoon characters, the darkened school auditorium (which also served as the cafeteria) where it was screened, and sitting next to a little girl named
Peggy F., who I had a crush on. Sadly, Peggy is no longer with us.
|
| The Righteous Mind -- Posted on Thursday, May 24 2012
|
 I've been in a political mood lately, so I'm not to be messed with. I've been in a political mood lately, so I'm not to be messed with.
I'm reading Jonathan Haidt's new book
The Righteous Mind: Why Good People are Divided by Politics and Religion,
and I'm truly trying to follow the author's logic. His basic thesis is that there are moral foundations to the human mind that are rooted—to some extent or other, depending on one's liberal, libertarian or conservative leanings—in a matrix of six primary concern areas: caring/harm; liberty/oppression; fairness/cheating; loyalty/betrayal; authority/subversion; and sanctity/degradation. This matrix corresponds left-to-right to the liberal—conservative mindset, where liberals tend to be concerned with the care and well-being of others and conservatives are concerned with authoritarian/patriotic allegiance and the sanctity of things like marriage and sexual relations.
Haidt, a noted professor of psychology and business ethics at the University of Virginia and New York University, is a leading researcher in the field of moral psychology. He likens our intuitional/rational behavior as a rider on an elephant, where the rider's purpose is to serve the elephant (Haidt isn't being political here; the elephant could just as easily be a donkey). What he means by this is that while considered, rational (System 2) thinking is just dandy, most human behavior is in fact based on intuitional (System 1) thinking, which is more immediate because it's a primordial, lower-brain (autonomic) way of dealing with the world. Thus, the logical, rational
(and therefore nuancing) rider serves the knee-jerk elephant.
Were it the other way. A lumbering behemoth that thinks only via autonomic, peripheral nervous responses is generally incapable of rational thought, and proceeds to get its way by physically plowing through the field of opposers. It in fact has no need of a rider, although Haidt attempts to screen this fact by supposing that the rider and elephant are somehow complementary (recall the good/bad Captain Kirk episode in the original Star Trek series). In the end, it simply doesn't work—Haidt would have us believe that the endless political and religious wars humankind has had to endure, spurred on by patriotic fervor, hypocritical self-altruism and envy, are simply unfortunate but necessary consequences to ultimately achieving mutual beneficial cooperation and a "righteous" existence. And even here he trips himself up:We are downright lucky that we evolved this complex moral psychology that allowed our species to burst out of the forests and savannas and into the delights, comforts, and extraordinary peacefulness of modern societies in just a few thousand years. Yeah, life on Earth is just one
damned delightful Eden, isn't it?
(Steven Pinker is an idiot.)
Here Haidt reveals not only his total ignorance of human history (we did not "burst out," it took hundreds of thousands of years of hunter-gatherer migration, while the transition to farming and agriculture took at least 10,000 years) but also his decidedly fundamentalist Christian belief system (Haidt's "few thousand years" sounds suspiciously like 6,000 years). Indeed, Haidt can't even get through the book's Introduction without treating his readers to a quote from the Gospel of Matthew.
Haidt can't say enough good things about religion, which he views as necessary for the communal adhesion of fellow co-religionists. But by this standard, a religion based on tree worship would be neither better nor worse than any other. I don't deny that religion has the ability to bind communities and make people feel good about their lives, but folks like me are really more interested in whether there's anything real behind religious beliefs (like God), not their ability to anesthetize people with a lot of ritual nonsense.
The book's biggest failure, however, is the author's inability or unwillingness to define "morality," which is odd given the book's topic on righteousness. Haidt tries, but the best he can do is something along the lines of "A set of values, beliefs, norms, practices, traditions and virtues that serve to regulate or suppress self-interest and make cooperative societies possible." By this definition, Nazi Germany was a moral society (in all fairness, Haidt acknowledges this, so he downgrades his definition to that of an adjunct to the definitions of unspecified others).
But I don't condemn Haidt for saying that in the end we must all find a way to get along, and he's dead right on that. And the book is not as narrow as I've probably painted it here. All I'm saying is that it would be nice if, just once in a while, rational thought would outweigh the more immediate gratification of mindless action and the violence that often accompanies it. After all, if we end up blowing ourselves to oblivion it will be the elephant, not the rider, who forces that plunge into the final insanity.
|
| Very Dark (Nonexistent) Matter? -- Posted on Wednesday, May 23 2012
|

This is the Bullet Cluster, a pair of colliding galaxies that serves as perhaps the best evidence astrophysicists have for the existence of dark matter.
So what exactly is dark matter? Nobody really has a clue. Theorists have massaged Einstein's gravitational field equations over and over again, while others
have proposed the existence of exotic, previously unseen
forms of matter like weakly-interacting massive particles and heavy neutrinos. Still others have proposed that dark matter doesn't really exist at all, it's just some
unexplained, erroneous artifact or glitch in the observations.
But it's definitely there.
Meanwhile, despite the recent (tentative) discovery of a new (but uninteresting) particle by the Large Hadron Collider, CERN's 6-billion dollar instrument hasn't found the Higgs boson (at an estimated 130 GeV, it should have been detected by now), nor has it detected any evidence for extra dimensions or expected supersymmetry particles like selectrons and photinos. It hasn't found any evidence for dark matter, either, nor has it created any mini black holes, those harbingers of destruction that conservatives warned us about two years ago.
While watching numerous National Geographic programs last month on the 100th anniversary of the sinking of the Titanic, I was struck by how little of anything is found at ocean depths exceeding only a mile or so. Not only are hydrostatic pressures immense at these depths, but there's no sunlight at all; the few creatures that live down there eke out a tenuous existence from the occasional sub-millimeter sized detritus that drifts down from above, or from the rare bite-size critter that happens by. In most parts of the world, the ocean floor is characterized as looking exactly like a desert.
What if the subatomic world at the LHC energy level is also a desert? What if there is no Higgs boson, no extra dimensions, no chaotic, seething quantum foam? What if the Planck-scale world (roughly \(10^{-35} \) meter) is completely barren? Scientists are already considering that possibility, at least in terms of the LHC's inability to detect anything, and their responses have typically been along the lines of "going back to the drawing board" and coming up with new theories. But a minority of others have suggested that, barring a reversal of fortunes, we may be staring at the end of physics.
Last night I watched the 1999 film
The Thirteenth Floor again (I seem to watch it about once a year), which deals with the nature of reality. It's not a perfect film, and I'm sure that Spielberg could do a better job, but the basic concept is fascinating all the same. Simply put, it raises the question of whether we're living in a computer-simulated world, programmed by future humans (or whatever). One way to test such a hypothesis would be to develop instruments that can see smaller and smaller distance scales. Presumably, at some tiny scale the programming of even the most sophisticated computer simulation would have to break down, and at that scale one would literally see nothing. And at that scale, one would literally have reached the limits of physical reality, or at least the limits of the computer program in its description of what would otherwise appear to be a perfectly real world.
Over the past ten years or so, I've read an enormous number of books on religion and religious philosophy, particularly on how these fields relate to hard science. It should come as no surprise to the few regular visitors of this website that mathematical symmetries and physical laws, especially gauge theory, demonstrate that a benevolent Creator must exist, despite the fact that an enormous amount of apparently needless human suffering and misery coexist with the beautiful creation that we see all around us and in the observable universe. An impersonal, wind-it-up-and-let-it-go Creator would seem to fit perfectly with such a reality, and I'm still struggling with the ramifications of this concept.
|
| Calculis for Morans -- Posted on Wednesday, May 23 2012
|
 The spelling's off, true (and they struggled with the word 'impossible'), but the Tea Partier who displayed this sign in Washington last week got the sentiment right—the federal 1040 return process is in desperate need of reform (unless your income is as pathetic as mine, in which case the 1040 EZ for Dummies can be used). Hermann Weyl, upon becoming an American citizen after leaving Germany for Princeton in late 1933, said as much himself: The spelling's off, true (and they struggled with the word 'impossible'), but the Tea Partier who displayed this sign in Washington last week got the sentiment right—the federal 1040 return process is in desperate need of reform (unless your income is as pathetic as mine, in which case the 1040 EZ for Dummies can be used). Hermann Weyl, upon becoming an American citizen after leaving Germany for Princeton in late 1933, said as much himself:Our federal income tax law defines the tax \(Y\) to be paid in terms of the income \(X\); it does so in a clumsy enough way by pasting several linear functions together, each valid in another interval or bracket of income. An archeologist who, five thousand years from now, shall unearth some of our income tax returns, together with relics of engineering works and mathematical books, will probably date them a couple of centuries earlier, certainly before Galileo. (Weyl made this statement in 1940, so his use of "Our" rather than "Your" would have been appropriate by then.)
However, my mind is totally at odds with the
39% tax rate that is applied to the very wealthy in this country today. Back when Eisenhower was in office, the highest tax rate was set at a staggering 91% of gross income. Coupled with the fact that the number of truly rich people was a fraction of what it is now, and that the money was used to help support a population of only 150 million people, makes me think that the wealthy in this country never had it as good as it is today.
But Republican law makers are clamoring for lower taxes on the rich, and rates as low as 25% and even 15% are being bandied about. Ayn Rand fans will understand my little joke about "Who is John Galt and why the hell should he pay any taxes at all?" and perhaps feel that a negative tax rate would be appropriate for the wealthiest Americans. That is, they should be paid just to exist (just think of the job creation!) Meanwhile, we have statements like that of Goldman-Sachs CEO Lloyd Blankfein, who infamously reminded the unwashed of this country that "We're doing God's work." Rand was a virulent atheist, but I think a sly smile broke out on the face of her corpse when those words were uttered.
But of course all this Tea Party crap is just a subterfuge. That much is obvious, given the fact that a majority of Republicans and Tea Partiers actually stand to lose income and benefits by supporting lower taxes for the patricians among us (somebody's gotta pay if the country's going to keep running). And that's why the recent re-emergence of the Obama birther issue is so transparent. Bless their little hearts, the Republicans and their more virulent TP offspring have exhibited notable self-control to date, but that's only because that can't say out loud what's actually in those hearts. Remember, the Tea Party sprang up out of nowhere only a few months after Obama had taken the oath of office; by April 2009 he'd done nothing but talk, but already the Tea Partiers were threatening to bring down the government over taxation, religious freedom, the right to wolf down fried Twinkies and a host of other Very Important "heartland" issues over which they had been quiet as church mice under W's majestic spell.
So I'm forced to reveal here exactly what's in those hearts, which is simply this: "There's a nigger in the White House, and we're not going to stand for it." No other explanation is possible.
My prediction is that upon Obama's departure, either through replacement by Mitt Romney, term limits or assassination (those little hearts are beating faster now),
the Tea Party will evaporate into nothingness. Until then, we're stuck with all this crap about birtherism, Kenyan Marxist hatred for America, over-taxation of the über-wealthy, and elitist liberal sniggering over fried Snickers bars and the country's 35% obesity rate.

krugman@nytimes
|
| Lincoln Again -- Posted on Tuesday, May 22 2012
|
 Lincoln at Antietam battlefield, October 1862. At 6 feet 4 inches, he was our tallest Chief Executive. Lincoln at Antietam battlefield, October 1862. At 6 feet 4 inches, he was our tallest Chief Executive.
A while back I mentioned a medical book devoted to the physical characteristics of Abraham Lincoln and how the book's author, Dr. John G. Sotos, MD, attempted to conduct a (very) post-mortem analysis of our 16th president. Here I'll just mention that
National Geographic Explorer recently aired a program examining Dr. Sotos' investigations, and it was very interesting. You can watch the one-hour YouTube program at the link if you like, but you should really read the
book itself—you'll learn just about everything you ever wanted to know about Lincoln and his physical ailments (he most likely contracted siphyllis, lost a chunk of his jawbone during a botched tooth extraction in 1841, took highly toxic blue mass mercury pills for constipation, and might have already been dying of multiple endocrine neoplasia type 2b when he was assassinated). While the author reveals little about the sex life of the President and First Lady Mary Todd Lincoln, I really do think it's all for the best.
By the way, Dr. Sotos emailed me to state that he recently sat through four lectures on Hermann Weyl's Symmetry book, which pleased me no end, and that he originally considered majoring in mathematics. But he also used the occasion to educate me on a few medical misstatements I made in my March 28, 2012 posting. I guess it's bad enough that I studied physics ...
|
| Incomprehensible -- Posted on Tuesday, May 22 2012
|
 A nice photo of a young Hermann Weyl, undated but probably 1913 A nice photo of a young Hermann Weyl, undated but probably 1913
This month marks the 120th anniversary of the theoretical discovery of the electron by Hendrik Antoon Lorentz, a Dutch physicist who was Einstein's idol. Indeed, Lorentz actually derived the space-time transformation equations of Einstein's special relativity theory several years before Einstein's famous 1905 Annalen der Physik paper, though Lorentz did not fully appreciate what he had discovered. But, as the article in
Scientific American describes, Lorentz' formulation of the electron theory in 1892 is a nearly incomprehensible mishmash of mathematical symbols, totally unrecognizable (at least by me) today. It reminds this writer of the work of James Clerk Maxwell, whose 1860s formulation of the famous Maxwell equations of electrodynamics is almost completely buried under a bizarre tangle of abstract mathematics and graphics describing spinning lines of force and fields. It wasn't until 1874, when the eccentric, self-taught English mathematical physicist Oliver Heaviside, overcome by a lecture on Maxwell's work, retired to a room of his parents' house to begin an austere, unmarried life of solitary scientific research that produced, among other notable discoveries, the first clarified exposition of Maxwell's equations in the vector form that we all know and love today.
And so it was with me, having spent the last few weeks trying to decipher Hermann Weyl's earliest work on general relativity, all neatly encapsulated in the first two volumes of his four-volume Gesammelte Abhandlungen. I was looking for interesting tidbits that might expand my understanding of the man's work, particularly his 1921 paper that supposedly introduced the concept of wormholes to a world still too shaken by a world war and the hyper-inflation it wrought on Germany for anyone to truly grasp or appreciate. Well, 90 years on I find that I could not grasp it, either—Weyl's mathematics is just too abstract for my poor brain, though his physics papers are exemplary in their mathematical clarity (even in German).
I recently finished Constance Reid's 1996 biography on
David Hilbert, the great German mathematician who was Weyl's undergraduate mentor and 1908 PhD advisor at the University of Göttingen. The book itself is fairly non-technical but does describe in some detail Einstein's mathematical wanderings (bewilderment might also be applicable) en route to his famous November 1915 exposition on general relativity. Reading this (and other historical descriptions of Einstein's effort) gives one the impression that at times Einstein was a total idiot. By comparison, it was Hilbert, hot on the trail of the GR theory himself, who derived the correct field equations from a variation of the Lagrangian \( \int \sqrt{-g}\, R\,d^4 x\), which today is known as the Einstein-Hilbert action (it should be the other way round). Einstein got the equations after a laborious, circuitous route in which he invested many months of paper and ink, whereas Hilbert got them in less than five minutes.

Photo of Hilbert with Weyl in the garden of the former's home, taken around 1925
I could also relate a similar story about Erwin Schrödinger, whose 1926 derivation of his famous wave equation was complicated by the fact that the noted Austrian physicist could not actually solve it for the hydrogen atom! He appealed to his close friend and colleague Weyl (both were still at the Swiss Federal Technical Institute in Zürich at the time), who immediately produced the solution (it still puzzles me that the equation is not called the Schrödinger-Weyl wave equation, but what the hell). [Somewhere on this site I've included a link to Schrödinger's original 1926 paper, which is about as comprehensible to me as Maxwell's original EM theory. Good luck with it.]
It is a testament to these early theorists that they had the brains to understand papers that today are considered incomprehensible. But it's all they had to work with.
|
| Dangerous Theory Declassified -- Posted on Monday, May 14 2012
|

From the introduction to Rainich's 1925 paper. See below.
The 1st and 2nd editions of Adler, Bazin and Schiffer's Introduction to General Relativity (1965, 1975) are favorites of mine, mostly because I used them to learn general relativity. But the latter text also has a chapter on unified field theory that includes a very detailed mathematical description of the so-called already-unified theory of Rainich, Misner and Wheeler, whose ideas span roughly from 1925 to 1963. Based primarily on the fundamental matrix properties of the
tensors associated with general relativity and electrodynamics, the theory demonstrates fairly convincingly that the electromagnetic stress-energy tensor \(F_{\mu\nu}\) can be viewed simply as a mathematical artifice used to make the solution of Einstein's gravitational field equations tractable. Indeed, the theory parallels the idea of using the basic Cauchy-Riemann conditions of analytic complex analysis to immediately solve the homogeneous Laplace equation \(\nabla^2 \varphi(x,y) = 0 \) for two dimensions. In the opinion of Rainich, Misner and Wheeler, \(F_{\mu\nu}\) is a purely fictitious quantity that has no independent meaning outside the overall metric structure of space-time.
The presentation of the theory in the text is based on a simplified derivation of the equations that Menahem Schiffer and Ronald Adler performed sometime prior to 1963 (A new derivation of the equations of the already-unified field theory). Amazingly, they included their derivation in the book only after it had been declassified by the Department of Defense!
The declassified document can be found at the link given
here. Why on Earth the Defense Department might have taken interest in the theory boggles the mind, but I can offer one plausible explanation.
You may remember reading a novel back in the 1970s called The Philadelphia Experiment in which the protagonists accidentally transport themselves back in time to some US battleship preparing to set sail during World War II. I recall nothing other than that, other than it being an interesting story about the possible military applications of time travel. But prior to that, I distinctly recall reading about a plan the Pentagon tried to develop in the 1950s involving the possibility of exploding an atomic bomb in the past. (I have Googled this concept and found nothing. Is my memory going out on me? Has the US military pulled all references of the study off the Internet? Am I becoming paranoid? Lupus! Is it Lupus?!)
Of course, the successful demonstration of this idea would have many practical military uses, although the usual problem of causality would remain: Tom: "Did you hear that the Pentagon destroyed Russia back in 1917 with time-traveling nuclear weapons?"
Dick: "What's a Russia?"
PS: George Yuri Rainich was apparently the first mathematician to examine the Einstein and Maxwell equations from a purely algebraic and matrix approach. He presented his first results back in 1925 (you can download the paper
here). Noted Princeton physicist John Archibald Wheeler and his doctoral student Charles Misner extended these results in 1957. But to really understand the theory (it's all just algebra, but it's fairly convoluted), you should read the Adler-Bazin-Schiffer text.
|
| Weyl's Theory -- Posted on Friday, May 11 2012
|
 A lot of research is being conducted today regarding the dark matter (DM) and dark energy (DE) problems. It would appear to many researchers that these issues cannot be resolved by considering DM and DE to be merely some geometrical consequence of Einstein's general relativity (GR), so attention has been focused on the possible existence of new fields, with GR acting as a space-time bystander. Just what these fields may be no-one knows, but hypothetical critters like weakly-interacting massive particles (WIMPS) and new kinds of neutrinos have been suggested. A lot of research is being conducted today regarding the dark matter (DM) and dark energy (DE) problems. It would appear to many researchers that these issues cannot be resolved by considering DM and DE to be merely some geometrical consequence of Einstein's general relativity (GR), so attention has been focused on the possible existence of new fields, with GR acting as a space-time bystander. Just what these fields may be no-one knows, but hypothetical critters like weakly-interacting massive particles (WIMPS) and new kinds of neutrinos have been suggested.
Against this background seem to be never-ending theories involving Weyl's 1918 gauge theory, in various forms and disguises. As I've said or implied many times before, it's neat that Weyl's work continues to play an important role in current quantum-mechanical and cosmological research, but it's also strange because the theory was effectively killed off over 90 years ago.
Today I bring to your attention two papers involving Weyl's early work. The first, from February of this year, is called
Weyl-Cartan-Weitzenböck Gravity, written by Zahra Haghani and colleagues, all from Iran and China, but surprisingly very well written. The paper takes Weyl's theory and adds torsion, which just means that Weyl's connection term is non-symmetric. Torsion was introduced by Élie Cartan (1869-1951), the French mathematician (photo) who introduced the idea of a non-symmetric affine connection (\(\Gamma_{\mu\nu}^\alpha \ne \Gamma_{\nu\mu}^\alpha \)) sometime in the 1910s, I believe. Einstein seemed to have gotten hooked on the idea around 1925 and never let go of it. His final calculations, discovered on the floor of the hospital bed where he died in 1955, are riddled with the things, which Einstein believed held the key to a workable unified field theory (but in fact were a total waste of time, not to say talent). At the same time, I've never heard of Weitzenböck — probably just another umlauted German; I haven't the energy to Google him. But the Haghani paper is very readable, interesting even, though to me it serves as yet another example of how, when you generalize something to allow for more variables (i.e., torsion), you get a theory that arguably explains everything and nothing at the same time.
Included in the paper's citations are several works by Mark Israelit of the University of Haifa. Israelit has probably written as much about Weyl-related theories as anyone. He has even written a book called
The Weyl-Dirac Theory and Our Universe (for the life me, I can't see paying over a hundred bucks for a 160-page book about an obscure theory). The reference to Dirac has to do with his famous
1973 paper, in which he tried to explain a few of the mysteries of the universe via yet another take at Weyl's theory (no really, it's a great paper and you should read it). My local library and Caltech were unable to acquire Israelit's book for me (yes, I have no life), but another work of his that supposedly summarizes everything he has to say in the book can be found
here.
|
| Weyl on Mathematics and Physics -- Posted on Monday, April 23 2012
|
Quantum theory has gone even a step further. It has shown that the observation always amounts to an uncontrollable intervention, since measurement of one quantity irretrievably destroys the possibility of measuring certain other quantities. Thereby the objective Being which we hoped to construct as one big piece of cloth each time tears off; what is left in our hands are — rags. This Heisenberg-like quote is from Hermann Weyl's 1954 address to New York's Columbia University, in which Weyl—nearing the end of his life—elected to speak on the unity of knowledge. In his talk Weyl spoke about how truth is ascertained rather directly by mathematical proof, while in physics it is obtained through the somewhat more involved process of experimental and observational evidence. Even so, truth is truth, and however it is obtained impacts human consciousness regardless of the road taken, for truth
necessarily distinguishes itself in a "before" and "after" sense to the human mind by being what Weyl calls in German aufweisbar (demonstrable).
I used to think that the physical act of observation, which conventionally results in the collapse of the system's wave function to a particular eigenstate, must somehow involve the human mind, and that therefore human consciousness and the quantum state of the world are inexplicably connected. The great British mathematical physicist Roger Penrose has asserted that this is not quite the case, although he does believe that human consciousness has a quantum basis. Whatever the hell is going on, it still ends up with the mind in possession of information it didn't have before the observation.
Having now read Weyl's talk, I wonder if the same thing occurs when the human mind successfully completes a mathematical proof. True, there is nothing that "collapses" outside of the brain, but perhaps a collapse of sorts results in the mind itself. If the two phenomena—physical measurement and mathematical proof—are indeed essentially the same, then the concept of a world external to the mind would seem to have less of a concrete meaning. Weyl himself once stated that he believed there might not be any "there" there, and that the universe doesn't happen, it just "is."
Well, at least I think this is part of what Weyl was saying, as at the end of his talk he admits to being guilty of some philosophical "turbidity" that may leave the listener (in this case, reader) confused. To this reader, the only thing more obtuse than Weyl's pure mathematics is his philosophy, the larger subject of which I never studied in school and have never been able to master on my own.
Weyl was a first-rate human being, one of the most cultured, educated and learned of his time, whose interests not only spanned many difficult subjects but of which he also achieved mastery. Today we have many brilliant scientists and mathematicians whose mental capabilities rival (or may even exceed) his, but none can be considered as culturally accomplished as Hermann Weyl.
|
| Unitarity -- Posted on Monday, April 23 2012
|
Modern physics renders it probable that the only fundamental forces in Nature are those which have their origin in gravitation and in the electromagnetic field.
 In 1921 Hermann Weyl offered this opinion in his Nature article entitled "Electricity and gravitation." Today, 91 years later, we still do not know whether Weyl was being ignorant, näive or extraordinarily prescient. Five years after he made this claim, physicists began to realize that there were more than just two fundamental forces; today we know there are four. Actually, it's only three—the electroweak theory is supposed to have unified the weak nuclear and electromagnetic forces, though this fact is often neglected when discussions of the fundamental forces of nature are brought up. And now there's evidence that gravity may in fact be describable in terms of the strong nuclear force, reducing the total back down to two, as Weyl surmised. In 1921 Hermann Weyl offered this opinion in his Nature article entitled "Electricity and gravitation." Today, 91 years later, we still do not know whether Weyl was being ignorant, näive or extraordinarily prescient. Five years after he made this claim, physicists began to realize that there were more than just two fundamental forces; today we know there are four. Actually, it's only three—the electroweak theory is supposed to have unified the weak nuclear and electromagnetic forces, though this fact is often neglected when discussions of the fundamental forces of nature are brought up. And now there's evidence that gravity may in fact be describable in terms of the strong nuclear force, reducing the total back down to two, as Weyl surmised.
The May issue of
Scientific American provides a layperson's view of a new computational approach to particle physics called the unitarity method by its authors, Zvi Bern of UCLA, Lance Dixon of the SLAC National Accelerator and David Kosower of the French Institute of Theoretical Physics. They developed the method as a means of avoiding the avalanche of higher-order Feynman diagrams needed for calculations involving strong-force particle interactions. Simply stated, a Feynman diagram is needed for every conceivable interaction; for example, two electrons repel each other through the exchange of a single photon. But that photon might give rise to an electron-positron pair in mid-flight before coalescing back to a photon, and there's a Feynman diagram for that process as well. In fact, there are an infinite number of increasingly more complicated diagrams that are involved in simple electron-electron scattering. The calculation is made possible only by the fact that the probability associated with each higher-order diagram quickly grows exponentially smaller, so that the calculation can be safely stopped at some point with the desired degree of accuracy.
According to the unitarity method, only a tiny fraction of the calculations required by the Feynman-diagram approach is needed to get the same results. Even better, the method appears to allow for the inclusion of the gravitational force by assuming that a graviton behaves as a kind of gluon pair. If this approach is correct, unitarity would be a momentous discovery, as gravitation has up to now been considered non-renormalizable and hence unfit for quantum-mechanical theories.
I haven't seen any of the six references cited in the article, and I'd be willing to bet that I couldn't understand them, anyway. Still, it's neat to think that maybe Weyl was right all along.
Also in the May issue is the editorial article "Is supersymmetry dead?", which reflects on the negative results to date of the Large Hadron Collider's search for SUSY superpartners (at least the lighter ones). Is hasn't found any, making a lot of CERN physicists nervous. Although SUSY is based in large part on Weyl spinors, I'm hoping that it's a dead theory—but the real reason is that the theory is too hard for me to follow!
|
| An Inch Thick -- Posted on Thursday, April 18 2012
|
 I was in Vienna, Austria recently and visited the city's Kaisergruft (Kaiser crypt), the underground mausoleum where Emperor Franz Josef and his family are entombed. Vienna seems to have a strange fascination with death, and I don't really know why—perhaps it has something to do with the world wars, both of which devastated the city. At any rate, the crypt has about 150 people buried here in unbelievably ornate, above-ground bronze caskets, each weighing tons. They're truly works of art, with macabre simulated bones and skulls and such, and they all reflect the enormous wealth associated with the dead. Most are full burials, while some containers hold only the hearts of the deceased. Like I say, it's strange. I was in Vienna, Austria recently and visited the city's Kaisergruft (Kaiser crypt), the underground mausoleum where Emperor Franz Josef and his family are entombed. Vienna seems to have a strange fascination with death, and I don't really know why—perhaps it has something to do with the world wars, both of which devastated the city. At any rate, the crypt has about 150 people buried here in unbelievably ornate, above-ground bronze caskets, each weighing tons. They're truly works of art, with macabre simulated bones and skulls and such, and they all reflect the enormous wealth associated with the dead. Most are full burials, while some containers hold only the hearts of the deceased. Like I say, it's strange.
While his story is very interesting, that of Josef's wife is infinitely more so. Born in 1837,
Empress Elizabeth of Austria married Josef at the age of sixteen in what must surely have been (for her) an unwanted arranged marriage. Although he seems to have been a loving and devoted husband, Elizabeth, known as Sisi by close relatives, was a free spirit who hated the aristocratic life of elaborate state dinners and royal events. As one of the overseers of the Austrian-Hungarian Empire, she was herself sincerely devoted to Hungary and spent much time traveling there, but mostly to avoid court life. Out of desperation and boredom, she turned to the cult of beauty and physical fitness, spending many hours each day exercising, dieting and fussing with her face, hair and figure (she maintained a 19-inch waistline throughout most of her life). If Sisi reminds you of Lady Mary from Downton Abbey (my favorite TV show now), you're not alone.
The couple's living quarters was the famed H
apsburg Palace, also in Vienna, where I saw the actual apartments of Sisi, including her jewelry and many baths, makeup tables, beds and clothes. She took meticulous care of her teeth (which were not perfect) and the many exhibits include her dentist's cleaning tools. I tried to take a photo of her death mask, which shows a slight face with pits, but I was stopped by a zealous docent (nein, verboten). The couple's gold and silver dining sets are unbelievably extensive, valued at many millions of dollars, and I kept shaking my head at the ostentatious wealth that surrounded me and thinking of that line from Citizen Kane: "The loot of the world!"
But most interesting is the story of Sisi's death, which occurred in Switzerland in 1898 when the Empress was 60. While on a cruise on Lake Geneva, she went ashore to do some shopping and was attacked by an Italian anarchist. The incident itself was almost unnoticeable, her attacker seemingly only stumbling into her. But she collapsed and was rushed aboard her waiting yacht, where attendants noticed blood welling up under her corset. Her attacker had stabbed her with a thin, 4-inch file, penetrating her heart (ouch). In and out of consciousness, she repeatedly asked what was wrong. She then suddenly died, probably unaware that she had been murdered. Her husband Franz outlived her by 18 years.

Looking over Sisi's ornate casket, I couldn't help but think of Hamlet who, gazing at Yorick's skull, says
Here hung those lips that I have kissed I know not how oft.
Where be your gibes now? Your gambols? Your songs?
Your flashes of merriment, that were wont to set the table on a roar?
Not one now to mock your own grinning? Quite chap-fallen?
Now get you to my lady's chamber and tell her, let her paint an inch thick,
To this favour she must come; make her laugh at that!
|
| Weyl's Collected Works -- Posted on Thursday, April 18 2012
|
 I finally acquired the 4-volume set of Hermann Weyl's Gessammelte Abhandlungen (literally, "collected essays"), which includes papers written by Weyl from his immediate post-PhD days (1910) to shortly before his death in 1955. I was pleasantly surprised that not all of the papers are in German (I can read the ones in physics alright, but the math papers are a real bitch); some are in English, a few in French (which I can read), and fewer still are in Spanish (shame on me, I never learned the language, and every Californian should know it). Altogether it's around 3,500 pages, but of course I'm only interested in the physics articles, many of which give a keen insight into the the mind of Weyl and his physics. I finally acquired the 4-volume set of Hermann Weyl's Gessammelte Abhandlungen (literally, "collected essays"), which includes papers written by Weyl from his immediate post-PhD days (1910) to shortly before his death in 1955. I was pleasantly surprised that not all of the papers are in German (I can read the ones in physics alright, but the math papers are a real bitch); some are in English, a few in French (which I can read), and fewer still are in Spanish (shame on me, I never learned the language, and every Californian should know it). Altogether it's around 3,500 pages, but of course I'm only interested in the physics articles, many of which give a keen insight into the the mind of Weyl and his physics.
I didn't mean this to be another of my abominable books reports, but mostly as an excuse to post this photo of Weyl (taken about a month before his passing in December 1955, I believe) and to reflect on the sheer amount of mathematics and physics he accomplished in his relatively short (70 years) life. I was also looking for papers Weyl had published on wormholes, as he is generally credited with the concept, although my perusal so far of the Collected Essays hasn't revealed anything. When I come across it, I'll translate what I find and provide whatever comments are appropriate.
Lastly, I would love to quote some of Weyl's material here (especially his long and heartfelt tribute to fellow mathematician Emmy Noether on the occasion of her death in 1935), but I'm unsure of the associated copyright issues. I'm looking into it.
|
| The More Things Change -- Posted on Thursday, April 12 2012
|
|

If I'm wrong, then one would have been enough. — A. Einstein
I'm reading
The Attraction of Gravitation: New Studies in the History of General Relativity (J. Earman, M. Janssen and J.D. Norton, Editors; Birkhaüser, 1993), which is actually a fun read with many references to Hermann Weyl and his contributions to the theory. But the chapter that really caught my attention is
Hubert Goenner's A Hundred Authors Against Einstein, which addresses the criticism Einstein faced from opponents to his 1915 general theory of relativity. It is all the more fascinating given Goenner's detailed description of why the theory was opposed by so many in Germany (and the United States) as it relates to the political-cultural atmosphere that now exists in America today.
Although opposition to Einstein's theories began almost immediately (the special theory in 1905 and the general theory in 1915), the opposition didn't formally organize until after 1919, when the general theory was finally confirmed by the Principe solar eclipse measurements made by Eddington (although, to me, the theory's earlier explanation of the advance of perihelion of the planet Mercury is what really nailed it). Einstein himself believed the opposition was due to politics, although he could not have dismissed the possibility that, as a superstar of science, at least some of the criticism was the result of simple scientific envy. But as Goenner has it, criticism at the time seems to have revolved initially around one main objection: discomfort by many scientists with the sheer mathematical difficulty of the theory and an associated longing to maintain the relative simplicity of classical physics. While this is difficult for me to understand given the somewhat unimpeded acceptance of the emerging quantum theory of the time, I can understand how bizarre concepts such as time dilation and warped space-time might have seemed to skeptical older physicists.
At any rate, in 1931 a brief (104 pages) publication appeared in Leipzig entitled Hundert Autoren gegen Einstein (One Hundred Authors against Einstein, or HAE) that attempted to document the reasons why the theory was wrong. But by this time the Nazi Party was in the process of taking political control of Germany, and it greatly increased the purely antisemitic aspects of the criticism through an appeal to racist hatred and the promotion of Deutsche Physik, or "German physics." Since legitimate scientific questioning of the theory had been almost universally disproven, the "Relativity-theory-is-wrong-because-Einstein-is-a-Jew" argument grew; indeed, by 1936 relativity books were being burned in Germany, and posters bearing Einstein's picture with the words Noch ungehängt ("not yet hanged") were being circulated (although Einstein had left the country in 1933).
Goenner, a retired professor of theoretical physics at the University of Göttingen, rightly concludes that the criticisms leveled at Einstein's theories were largely championed by repressed, muddled-headed incompetents (although Johannes Stark, a Nobel prize winner, was an early Einstein opponent). However, he also notes with implicit alarm that HAE is a classic piece of evidence for the fact that the validation of a theory in the exact sciences can be achieved only from within the body of experts. What is required is a sufficient knowledge of the methods for gaining empirical data, for relating those data b
y self-consistent mathematical models, and for reaching public consent — always revisable — on the explicatory and predictive value of the resulting theory. By "public" here the public of scientists is meant. Acceptance or non-acceptance of the theory by the general public is irrelevant ... (my emphasis) At the conclusion of Goenner's paper he notes that, nevertheless, "the history of science cannot be separated from the general cultural and social environment." I take this to mean that while hard science may be the domain of eggheads, it is susceptible to a lay public whose political, religious and cultural prejudices can block acceptance of perfectly valid theories. The controversies surrounding evolution and global climate change serve as examples of such prejudice.
|
| Weyl Article -- Posted on Sunday, April 8 2012
|
Here's a lengthy but very informative introduction to the life work of Hermann Weyl by
John L. Bell, a mathematics professor at the University of Western Ontario. Written at the undergraduate level, it's short on mathematics but long on description, with an excellent list of references.
|
| Three Papers -- Posted on Wednesday, April 4 2012
|

Lieber Kollege! — Postcard dated 15 April 1918 from Einstein to Weyl, explaining E's argument with W's gauge theory. Einstein thought the theory beautiful (so schön) but he spotted a flaw. Einstein's little sketch at the bottom (which is mislabeled) shows that a vector parallel-transported over two different paths will vary both in length and time measurement as it is brought back to itself. This problem has bedeviled physicists now for 94 years. I got this photo from Prof. Norbert Straumann, who included it in his article Zum Ursprung der Eichtheorien bei Hermann Weyl, Physikalische Blätter, 43 (1987), Nr. 11.
Here are links to three recent papers on Weyl and his 1918 gravity theory. It never ceases to amaze me how the theory has persisted all these years, in spite of the fact that it was given up for dead 90 years ago. I believe this can be attributed either to a fascination that physicists continue to have for unified field theory, or just plain academic stubbornness. Another explanation would be the fact that Weyl's failed theory continues to fascinate simply because it is based on a beautiful mathematical symmetry whose questionable relevance to geometry, unlike its highly successful transplantation in quantum mechanics, remains open to speculation.
The first of these papers is from
Alexander Afriat (now with the University of Utrecht, I believe), who posits the idea that Weyl came across his theory while pursuing a kind of "mathematical justice." It is well known that the parallel transport of vectors generally results in a change in vector direction, depending on whether space-time is flat or curved. Riemannian geometry, in which the mathematical language that Einstein's gravity theory is couched, allows vector direction to vary but necessarily preserves a vector's length or magnitude. Afriat believes that Weyl saw this aspect of Riemannian geometry as not only a flaw but a mathematical injustice, and he explores this possibility partly as a consequence of Weyl's philosophical background (which was extensive). Reading Weyl's papers from the time, including his seminal Space-Time-Matter, my take is that Weyl was simply exploring a mathematical avenue that allowed for the generalization of Riemannian geometry. After all, Weyl and others at the time were already eager to unify the then-new theory of general relativity with electrodynamics, and I believe Weyl saw a way of doing that by allowing vector magnitude to vary from point to point as a consequence of a non-zero electromagnetic field. Consequently, I really don't see any sense of "justice" at work here, though I may have misunderstood Afriat's paper. At any rate, the paper is very readable and I recommend giving it a look.
The second paper is called "Weyl geometry in late 20th century physics" by
Erhard Scholz.
Dr. Scholz (University of Wuppertal) has probably explored Weyl's physics, mathematics, philosophy and life more than anyone living today, and his views on Weyl's work can be considered the gold standard on the man and his achievements, although Norbert Straumann of the University of Zürich might also have a claim at the title. Scholz explores Weyl's theory as it relates to several notable attempts to generalize general relativity beginning with the Jordan-Brans-Dicke scalar-tensor approach of the 1950s through more recent attempts to link Weyl's scale invariance idea with cosmology, in particular the dark energy/dark matter problem.
Scholz' paper is perhaps the best of its kind I've seen to date, because his paper succinctly and neatly summarizes why Weyl's theory remains of interest in modern physics.
Although Scholz doesn't address it in this paper, the Jordan-Brans-Dicke theory itself resulted from Weyl's initiation of the Large Numbers Hypothesis (championed by Dirac), which tried to explain why the huge number 1040 and its square and cube arise so often and so naturally in atomic and cosmological physics. The late physicist Robert Dicke was apparently the first to notice that the enormous quantity \(c^2 /G\) is very close numerically to \(M/R\), where \(M\) and \(R\) are respectively the estimated mass and radius of the universe. Since the solution to the Poisson equation \(\nabla^2 \varphi = \rho\) (where \(\varphi\) is a scalar function) is proportional to \(M/R\), Dicke believed that a scalar field might play a fundamental role in general relativity, and he put such a field in his action Lagrangian. Indeed, Dirac originated the idea that Newton's gravitational constant \(G\) might vary inversely with time over cosmological epochs, giving rise to the notion that gravity is actually weakening with time. Over the past 50 years, many, many theories have been proposed involving a scalar-tensor approach to general relativity. Perhaps the most recent is that of John Moffatt, whose
Modified Gravity is in fact a scalar-spinor-vector-tensor theory. The more the merrier, I suppose.
Last and latest (January 2012) on the tour is General relativity and Weyl geometry by
C. Romero and colleagues, who attempt to address the "fatal flaw" in Weyl's 1918—that of non-integrable, path-dependent vector magnitude. It was Einstein who, entranced by Weyl's theory but nevertheless grounded in physical reality, noted that some vector quantities (those associated with atomic spectral lines, etc.) must not change under physical transport. Weyl's prescription for vector length variation makes no allowance for such vectors—they all vary under physical transplantation, and Romero's paper makes an effort to correct this flaw. Again, a very readable paper and well worth looking at.
It is possible to make vectors absolute under parallel transport without resorting to any of these complicated theories, and Schrödinger was apparently the first to spot it. Regardless of how you want to define the affine connection \(\Gamma_{\mu\nu}^\alpha\), physical transport of an arbitrary vector \(\xi^\mu\) can always be expressed simply as
$$ 2L\delta L = g_{ \mu \nu ||\alpha} \, \xi^\mu \xi^\nu dx^\alpha \quad \quad \quad \quad (1)$$
where \(g_{\mu\nu||\alpha} \) is the covariant derivative of the metric tensor with respect to \(x^\alpha\). (Note that Equation (1) vanishes identically when the connection term is the same as the Christoffel symbol.) Weyl assumed that this non-metricity tensor could be expressed as \(g_{\mu\nu||\alpha} = 2 g_{\mu\nu} \phi_\alpha \), where \(\phi_\alpha\) is a vector that Weyl identified with the electromagnetic four-potential. Thus, in Weyl's geometry we have \(\delta L = L \phi_\alpha dx^\alpha\), so that every vector changes magnitude under parallel transport, whether it wants to or not. However, many important vector quantities (especially currents and other 4-vectors) are proportional to \(dx^\mu /ds\), so that (1) becomes
$$2L\delta L = g_{\mu\nu||\alpha} dx^\mu dx^\nu dx^\alpha $$
The simplest example of such a vector is the unit vector \(u^\mu = dx^\alpha/ds \) itself, whose magnitude is unity: \(1 = g_{\mu\nu}u^\mu u^\nu\). Certainly, this number cannot change under parallel transport! We can ensure that its
\(\delta L\) is zero if we assume that the tensor \(g_{\mu\nu||\alpha} \) has the peculiar cyclic symmetry property \(g_{\mu\nu||\alpha} + g_{\alpha\mu||\nu} + g_{\nu\alpha||\mu} = 0 \). Considering the symmetry properties of \(g_{\mu\nu}\), we can easily derive an identity for the non-metricity tensor:
$$g_{\mu\nu||\alpha} = 2g_{\mu\nu} \phi_\alpha - g_{\alpha\mu} \phi_\nu - g_{\nu\alpha} \phi_\mu $$
This tensor has precisely the same symmetry properties as the T-tensor that Schrödinger proposed in his wonderful little 1950 book
Space-Time Structure (see Equation 9.11), in which he derived what he considered to be the most general affine connection possible. Thus, any vector proportional to the unit vector \(dx^\alpha /ds \) (along with the vector \(\phi_\alpha \) itself) remains fixed under parallel transport. Conversely, the length of any other arbitrary vector will change according to
$$ L \delta L = L^2 \phi_\alpha dx^\alpha - g_{\mu\alpha} \xi^\mu \xi^\nu \phi_\nu dx^\alpha \quad \quad \quad \quad (2)$$
so that the change in a vector will depend in a complicated way on the vector itself. Needless to say, integration of (2) would be very difficult.
And now that you're all sound asleep, I bid you good day!
|
| Dirac and Lincoln, but Mostly Lincoln -- Posted on Wednesday, March 28 2012
|
It seems that some essentially new physical ideas are here needed. — Paul Adrien Maurice Dirac
The universe is not only stranger than we imagine, it is stranger than we can imagine. — J.B.S. Haldane
 As we await the Supreme Court's politically-motivated decision to strike down health care
as we know it in this country and set the stage for a Romney or Santorum win in November, it's nice to know that there are good medical books out there to
help with the self-diagnoses and treatments we'll soon all be performing on ourselves. As we await the Supreme Court's politically-motivated decision to strike down health care
as we know it in this country and set the stage for a Romney or Santorum win in November, it's nice to know that there are good medical books out there to
help with the self-diagnoses and treatments we'll soon all be performing on ourselves.
But Dr. John Sotos'
The Physical Lincoln is not one of them. Though steeped in often arcane medical terminology, this 800-page book deals with just one topic—the physical, medical, mental and morphological characteristics of Abraham Lincoln, our 16th President. Why Sotos decided to include the above quotes in his book is anybody's guess, but they're actually quite appropriate to the subject
at hand.
Lincoln and the Civil War have always fascinated me, and I have many books on both. Lincoln represents America's quintessential tragedy figure, not just because he was assassinated by a Southern racist (shades of 2012!) but
because he experienced so many other personal tragedies, not least among them being his marriage to nutbar Mary Todd Lincoln. All but one of his children died in childhood, but Lincoln suffered other disasters, notably the loss of his early love Ann Rutledge to typhoid. But I digress.
Sotos is well aware of Lincoln's chronic constipation, syphilis, frequent melancholy, numerous malarial and smallpox infections, facial asymmetry and legendary homeliness, but by investigating Lincoln at a new level of detail of almost agonizing completeness he arrives at the startling conclusion that Lincoln almost certainly suffered from multiple endocrine neoplasia type 2b (MEN2b), a pre-cancerous condition whose symptoms mimic those of Marfan syndrome. Indeed, Dr. Sotos argues convincingly that Lincoln would probably have died from cancer within a year of his death by assassination.
Sotos has tracked down nearly all available actual and anecdotal medical data on Lincoln, and he has also examined all of Lincoln's photographs for subtle morphological clues—skin, eyes, lips, the mole, ears, neck, hands, the asymmetrical skull, scars, wrinkles. His analysis is fascinating; through his minute examination of the physical Lincoln in this way, Sotos has essentially rewritten the pseudo-historical, idealized Lincoln and made the man far more accessible.
I don't know how long it took Sotos to write this ponderously long and dense book, but reading it will take almost as much time (and figuring out the notation he uses for his citations is also time consuming). I highly recommend it.
After his death, Lincoln was embalmed and packed off for a lengthy train ride back to his home town of Springfield, Illinois. The train stopped at many cities along the way, and Lincoln's body was displayed to thousands of mourners. Morticians attended the funerary trip but they could not completely prevent decomposition of Lincoln's corpse, noting with alarm at one point that Lincoln had turned black. They treated the face with rouge and white powder, and eventually Lincoln was deposited in a temporary holding tomb at Oak Ridge Cemetery in Springfield. Over the next few decades, Lincoln's body was stolen and recovered several times, much to the dismay of Lincoln's sole surviving child, Robert Todd Lincoln. Then the makeshift mausoleum holding Lincoln's casket began to fall apart. In 1901, a new mausoleum was constructed (the one you see today), and plans were made to re-entomb the President. But by then Robert had had enough—he ordered his father's body to be encased in a steel cage and buried under ten feet of concrete to prevent any further disturbance of the body.
But unknown to Robert Lincoln, workers in the burial detail decided to make sure that it was actually Lincoln's body in the casket. A local plumber was brought in, and he cut a small viewing port in the lead lining of the casket directly over Lincoln's head. The workers—seventeen people in all—each peered into the casket. They saw the darkened but
unchanged face of Lincoln, the mole intact, the head shifted to the side resting on a shrunken pillow, along with a mildewed flag and other materials. They then sealed the port and proceeded with the burial. One of the witnesses was 13-year-old Fleetwood Lindley, the son of one of the workers. The last surviving person to see the physical Lincoln, Lindley died in 1963. "It didn't scare me at the time," h
e said later, "but for several months afterward I slept with Lincoln."
I find it highly ironic and altogether fitting that in the end Abraham Lincoln, our greatest president, the emancipator of the slaves, had himself become black.
I first visited Lincoln's mausoleum in Springfield in October 2004. It was very crowded that day, and while entering the crypt I was accompanied by dozens of screaming, unaffected school children. But they quickly exited and I suddenly found myself completely alone with Lincoln. Emotionally overtaken by the occasion, I wept.
Out of me unworthy and unknown
The vibrations of deathless music!
'With malice toward none, with charity for all'.
Out of me the forgiveness of millions toward millions,
And the beneficent face of a nation
Shining with justice and truth.
I am Ann Rutledge who sleep beneath these weeds.
Beloved of Abraham Lincoln,
Wedded to him, not through union,
But through separation.
Bloom forever, O Republic,
From the dust of my bosom! —Rutledge headstone, Edgar Lee Masters
|
| The Weyl-Trefftz Solution -- Posted on Thursday, March 22 2012
|
Trefftz—yeah, I can't pronounce it, either.
Several years ago I managed to locate a copy of Erhard Scholz'
Herman Weyl's
Raum-Zeit-Materie: An Introduction to His Scientific Work. In addition to being a great reference on Weyl's monumental 1918 book (subsequently revised and reissued through five editions, and still available in print), Scholz, co-author Hubert Goenner and others explore the various early foundational contributions Weyl made to general relativity, including his work in cosmology. Also included is Scholz' overview of Weyl's 1918 gauge theory (in German) which, though perhaps of historical interest only today, amusingly keeps popping up in modern physics papers, particularly those posted on the non-refereed
arXiv.org website.

Is Amazon's price too steep for you? You can now get the book in Kindle format for about the same price. [Ouch!]
Anyway, Scholz' book also talks about the Weyl-Trefftz solution to one variant of Einstein's field equations, and while I'd never heard of it, I recognized the solution itself.
Shortly after Einstein's general relativity theory was announced, Weyl began to look for generalizations of the theory. For Einstein's vacuum field equations with a cosmological constant \(\Lambda\),
\( R_{\mu \nu} - \frac{1}{2}g_{\mu\nu}R + \Lambda g_{\mu\nu} = 0 \)
Weyl discovered that the exact static solution is
\( ds^2 = e^\nu c^2 dt^2 - e^\lambda dr^2 - r^2 d\theta^2 - r^2 \sin^2 \theta\ d \phi^2 \)
where
\( e^\nu = e^{-\lambda} = 1 + 2M/r - k r^2 \)
which is very similar to the Schwarzschild solution (\(k = 0 \)). (Weyl's solution, also called the Weyl-Trefftz solution, had in fact been derived by numerous investigators.) The term involving \(kr^2 \) may or may not be important in understanding the problem of dark energy, and it is largely for this reason that dark energy and the cosmological constant are often spoken of as being one and the same.
So just who the hell was Trefftz? I found that the University of Dresden had an Erich Trefftz in 1920, but he was a professor of engineering mechanics, not physics. However, Erich had a daughter, Eleonore Trefftz, who was a physicist. But she was born in 1920 and, unless she was an infant prodigy, Eleonore Trefftz could not have been working with Weyl in the early 1920s. (By the way, Eleonore is
still alive and living in Germany. In 1956, she became the first female director of the Max Planck Institute.)
One more interesting tidbit. If we contract Einstein's equations with the metric tensor \(g^{\mu\nu}\), we find that \(R = 4\Lambda\). We can then rewrite the field equations as
\( R_{\mu\nu} - \frac{1}{4} g_{\mu\nu} R = 0 \)
When the Ricci scalar \( R \) is a non-zero constant, these equations are the same as those derived from the Weyl Lagrangian \(\sqrt{-g}\, R^2\), which he derived from his failed 1918 gauge theory. The solution to the
Weyl-Trefftz equation is of course the same as that given for \(e^\nu \) and \(e^\lambda \) above.
Most of the Scholz book can be read for free on
Google Books.
|
| Relativity Reaffirmed -- Posted on Thursday, February 23 2012
|
Scientists at the Gran Sasso Laboratory in Italy now say that the faster-than-light neutrinos they preliminarily reported in September were probably not superluminal after all. A
faulty fiber-optic cable, used to convey GPS signals for the time-stamping step, was likely to blame, although further tests are necessary to confirm the error.
Meanwhile, you might want to check out the religiously-motivated Conservapedia article on
relativity, which was quickly modified last September to include the faster-than-light story as proof that Einstein's 1905 theory is just balderdash (you see, action at a distance must be preserved at all costs in the tiny brains of conservatives, otherwise God would have no way to effect His miracles).
Conservapedia, a rabidly conservative website that mirrors the supposedly godlessly liberal Wikipedia, is a product of conservative gadfly Phyllis Schlafly and her idiot son Andy. It at least makes for humorous reading. The section on mass increase with velocity is especially entertaining, as it was quickly rewritten to reflect the fact that it is the four-momentum, not mass, that is velocity dependent.
A more recent experiment also shoots down the notion of superluminal neutrinos.
|
| Sigma -- Posted on Thursday, February 9 2012
|
Here's a
report stating that, unofficially, the Higgs boson has been confirmed to within 4.3 sigma (\( \sigma \)) at the Large Hadron Collider (LHC). The report adds that this corresponds to a signal that is 99.996% reliable.
 So what's a sigma? It's one standard deviation of area under the unit-area curve
\( (2\pi)^{-0.5} \exp (-0.5 z^2) \), or about 0.68 (68%). 2-sigma corresponds to about 95%, which is what the LHC was reporting two months ago for the Higgs. So is 99.996% more or less a certainty that the Higgs has been discovered? Not at all, because scientists typically want 5 sigmas (about 99.9999%) before they're willing to announce anything. That's a figure that corresponds
to an uncertainty of less than one part in a million. So what's a sigma? It's one standard deviation of area under the unit-area curve
\( (2\pi)^{-0.5} \exp (-0.5 z^2) \), or about 0.68 (68%). 2-sigma corresponds to about 95%, which is what the LHC was reporting two months ago for the Higgs. So is 99.996% more or less a certainty that the Higgs has been discovered? Not at all, because scientists typically want 5 sigmas (about 99.9999%) before they're willing to announce anything. That's a figure that corresponds
to an uncertainty of less than one part in a million.
But, as Caltech's Sean Carroll
points out, the last 14 Super Bowl coin flips have gone in the NFL's favor. Not counting the first flip (which has to be something), that has a probability of \( 2^{-13} \), which is about \(1.22 \times 10^{-4} \), or roughly 3.8 sigma of not happening. So is the Super Bowl rigged? Is all this talk about sigma just nonsense?
The Super Bowl is not rigged. What we've witnessed is just a highly unlikely happenstance. And at next year's Super Bowl, the probability that the NFL will get the coin toss yet again still stands at 50%, since chance is not cumulative (in spite of what you Las Vegas high-rollers think). To reach the 5-sigma threshold, the NFL would have to get the toss 18 times in a row, about the same probability of a Phyllis Diller wardrobe malfunction.
(By the way, the 99.996% reliability figure actually corresponds to 4.1 sigma, not 4.3, but who cares.)
Once is happenstance, twice is coincidence, three times is enemy action. — Auric Goldfinger
|
| The Ultimate Free Lunch -- Posted on Wednesday, February 8 2012
|
 Some months ago I posted an article about Arizona State University's Lawrence Krauss, the astrophysicist who is the author of eight books, including The Physics of Star Trek (which I didn't much care for). He's now got another, far better book out called
A Universe from Nothing: Why There is Something Rather than Nothing. It's kind of a printed version of his
YouTube lecture of the same name (the Internet version has been viewed nearly a million times), and he tells many of the same stories and jokes in both the book and the video. But the book provides greater depth, and some of the more involved topics he addresses in the video are made much more accessible in the text. Some months ago I posted an article about Arizona State University's Lawrence Krauss, the astrophysicist who is the author of eight books, including The Physics of Star Trek (which I didn't much care for). He's now got another, far better book out called
A Universe from Nothing: Why There is Something Rather than Nothing. It's kind of a printed version of his
YouTube lecture of the same name (the Internet version has been viewed nearly a million times), and he tells many of the same stories and jokes in both the book and the video. But the book provides greater depth, and some of the more involved topics he addresses in the video are made much more accessible in the text.
Not to spoil the book, but the main point Krauss makes is that the ever-expanding (and accelerating) universe, with its ordinary matter and dark matter/dark energy complement, is nevertheless flat in the general relativistic sense (that is, it is neither open nor closed), and because of this fact the universe's total energy content is almost certainly exactly zero. Krauss argues that radiation and matter are composed of positive energy (rest-mass, kinetic, electromagnetic, etc.), while gravitational fields consist of negative energy. Krauss uses a simple argument to explain this point: the datum for gravitational potential energy is purely arbitrary, and can be assigned to the surface of the Earth, the edge of the universe, or anywhere else, for that matter.
In high school we learn the terrestrial potential energy formula \( U = mgh \), with \( U = 0 \) taken at the Earth's surface, while college teaches us that it is \( U = -GMm/r \), so that \( U = 0 \) at \( r = \infty. \) Because potential energy gets increasingly more negative as \(r \) decreases, the negative energy of gravity increases. Krauss notes that it only takes a 4th-grader's intuition to make the inspired guess that the total energy content of the universe (positive plus negative) is probably zero. Only a flat universe could accommodate such a neat balancing act, and Krauss argues compellingly that this is exactly what the latest observations of the cosmic microwave background (and its attendant last scattering surface) are telling scientists. Thus, the universe begins with zero energy (nothingness) and maintains this zero energy content in spite of the fact that it is made of stuff today. All thanks to gravity, a force that nobody really understands, at least at the quantum level.
[None of this is entirely new; another, older (1998) book, Alan Guth's
The Inflationary Universe covers much of the same ground, but it did not have the benefit of recent cosmological discoveries.]
Krauss' book is not quite a popular treatment of the subject matter. It contains no equations, but some of the graphs require some thought to fully appreciate. If you enjoyed his YouTube talk, you'll love his book.
Update— I finished the book yesterday. Krauss asserts that the dark energy question is the most profound mystery in physics today, with scientists still stumped as to what it is and why it is causing the expansion of the universe to accelerate. As a layperson, I tend to go back to Einstein's field equations of gravity which, with the cosmological constant \( \Lambda \) included, are \( R_{\mu\nu} - 1/2 g_{\mu\nu} R + \Lambda g_{\mu\nu} = -8 \pi G/c^4 T_{\mu\nu} \). Even without \( \Lambda \), the elliptical orbits of planetary bodies precess, and I ask: What mysterious force causes this precession? The answer is that there is no force— perfectly uniform elliptical orbits occur only in Newtonian gravitation, while Einsteinian dynamics makes them precess as a consequence of the field equations. They precess because that's how relativistic gravity works. Using this analogy, I then ask myself why dark energy, which could be just one aspect of the cosmological constant, is considered so mysterious. What am I missing? Perhaps there is a discrepancy between the percentage of dark energy estimated for the total energy of the universe (about 73%) versus the estimated size of \( \Lambda \) that tells the experts something is not adding up right. Interesting.
|
| Digital Universe -- Posted on Tuesday, January 24 2012
|
The cover story of the February issue of Scientific American talks about a planned experiment at Fermilab designed to discover whether or not space-time is intrinsically digital. For many years, physicists have speculated on the possibility that, as one goes from ordinary distances to the tiniest scales, space-time goes from being uniformly smooth and continuous to being foamy or granular, composed of discrete "particles" of space that cannot exist at any smaller scale. Physicists have assumed that if this is true then space-time at this scale is in reality a violent, seething ocean swarming with virtual particles that go into and out of existence on time intervals approaching the fundamental Planck scale (`10^-44 ` second), resulting in a random, jittering hodgepodge of matter, radiation and space.
However, the experiment's designer,
Craig Hogan of the University of Chicago, thinks that this might not be the ultimate makeup of the universe. Hogan thinks that it is possible that at such small distances space-time is digital, being composed essentially of quantum bits of information—the fundamental 0's and 1's of the universe. In such a universe, Hogan believes, the two most basic theories of physics—quantum mechanics and gravitation—would be hopelessly irreconcilable because, at the smallest scales, "both break down into gibberish."
Hogan's experiment will rely on the output from two laser interferometers. As I understand it, laser light in one interferometer will be divided by
a beam-splitter and directed along two perpendicular paths of equal distances toward reflecting mirrors. The returning beams will then be rejoined and examined to see if there is any trace of interference. A separate, similar laser interferometry apparatus located nearby will produce is own interference pattern. If the two apparatuses do indeed detect interference patterns and, if the patterns are identical, Hogan believes this will confirm that space-time is indeed digital. Part of the difficulty in the experiment will be to ensure that the light paths are equal down to a gnat's backside; if they are, then any interference exhibited by the enjoined beams would presumably be due to the background "jitter" of space-time, in itself caused by its own "pixelation." Unlike the random jittering of granular space-time, pixelation would exhibit the same pattern from point to point in space.
This is fascinating, because many physicists believe that information must be the ultimate stuff of the universe. Some scientists, like Stanford's Leonard Susskind, believe that all information is encoded on hyperspace membranes, such as the spherical and elliptical surface areas of static and spinning black holes. Furthermore, Susskind believes, all information generated in or by the universe can never be lost or destroyed, so it has to be stored somewhere (check out the "Hawking information paradox" on Wikipedia for details).
I find Hogan's experiment particularly interesting because I believe, if confirmed, it would give credence to the possibility that we are living in a gigantic computer simulation.
Consider this (hardly original!): Assume that in the distant future advanced humans or other intelligent beings have developed computer simulation software that is so finely detailed it cannot be easily distinguished from reality (whatever that might be). Creatures simulated by the computer would have sentience and even free will, but would be unaware that they are being observed or studied (perhaps for entertainment or experimental reasons). These simulated creatures might even be designed to progress to the point where they would begin to construct complex machines to explore their universe, from the farthest reaches of their space to the quantum realm. However, no matter how detailed the simulation, at some microscopic distance it would have to break down, resulting in pixelation. There would be no "unified field theory," or any consistent fundamental physical theory at all for that matter, because ultimately it's all gibberish. The unification work that Einstein, Weyl, Pauli, Eddington and countless other simulated scientists had struggled with over the past 100 years would all be for naught, because unification doesn't exist.
Hey, I said consider it; I don't really believe it. But it's a fascinating idea, all the same. You might want to check out the 1999 film
The 13th Floor (I've written about the movie here before) in which two brilliant computer scientists (Armin Mueller-Stahl and Craig Bierko) make a truly frightening discovery.
|
| Gordan or Gordon -- Posted on Sunday, January 8 2012
|
 It has been brought to my attention that on one or two occasions I have confused the German mathematician Paul Gordan (1837-1912, shown) with the German physicist Walter Gordon (1893-1939). To set the record straight, Paul Gordan was the PhD advisor to another noted German mathematician, Emmy Noether, and it was Gordan who worked with (yes, another noted German mathematician) Rudolf Clebsch to produce the Clebsch-Gordan coefficients (which no sane physics student enjoys learning about or using). It was the German physicist Walter Gordon who worked with the Swedish physicist Oskar Klein to produce the famous Klein-Gordon equation in 1925. Please make a note of it! It has been brought to my attention that on one or two occasions I have confused the German mathematician Paul Gordan (1837-1912, shown) with the German physicist Walter Gordon (1893-1939). To set the record straight, Paul Gordan was the PhD advisor to another noted German mathematician, Emmy Noether, and it was Gordan who worked with (yes, another noted German mathematician) Rudolf Clebsch to produce the Clebsch-Gordan coefficients (which no sane physics student enjoys learning about or using). It was the German physicist Walter Gordon who worked with the Swedish physicist Oskar Klein to produce the famous Klein-Gordon equation in 1925. Please make a note of it!
By the way, while I could not find a photo of Walter Gordon, you might be interested to know that the
Emilio Segrè Visual Archives has tons of photos of famous scientists. (Look, but don't copy, as they're all copyrighted.)
|

 She did not forget Jesus!
She did not forget Jesus!
 As I have related before, post World War I Germany was very liberal, Berlin in particular, and Hermann Weyl, German-born but teaching in Zürich
at the time, was himself quite caught up in the liberal spirit. While helping his close friend and fellow ETH colleague Erwin Schrödinger solve the
latter's famous wave equation in 1925, Weyl did double duty wooing Schrödinger's wife Anny (the Schrödingers had a famously open
marriage, and the 1933 Nobel physics prize winner developed his wave equation while "on sabbatical" in the mountains with another woman). And how
did Weyl's wife, Hella, feel about all this? She herself was fooling around with ETH physicist Paul Scherrer, probably with Hermann's knowledge, if not
approval. Liberal, indeed.
As I have related before, post World War I Germany was very liberal, Berlin in particular, and Hermann Weyl, German-born but teaching in Zürich
at the time, was himself quite caught up in the liberal spirit. While helping his close friend and fellow ETH colleague Erwin Schrödinger solve the
latter's famous wave equation in 1925, Weyl did double duty wooing Schrödinger's wife Anny (the Schrödingers had a famously open
marriage, and the 1933 Nobel physics prize winner developed his wave equation while "on sabbatical" in the mountains with another woman). And how
did Weyl's wife, Hella, feel about all this? She herself was fooling around with ETH physicist Paul Scherrer, probably with Hermann's knowledge, if not
approval. Liberal, indeed.  I have ants in my pants today. Must be my imminent 64th
birthday (December 21) and the concurrent end of the world on that date, as the Mayans predicted. It's also the shortest and darkest day of the
year. Well, it's been a good life.
I have ants in my pants today. Must be my imminent 64th
birthday (December 21) and the concurrent end of the world on that date, as the Mayans predicted. It's also the shortest and darkest day of the
year. Well, it's been a good life. 

 \(\leftarrow\) Detail of Einstein's April 1918 postcard to Weyl, outlining E's objection to W's theory
based on the time difference that an arbitrary vector would experience when transported over two differing spacetime paths. In Weyl's theory, the rate of a ticking
clock, as well as the total time difference, depends on the vector's past history.
\(\leftarrow\) Detail of Einstein's April 1918 postcard to Weyl, outlining E's objection to W's theory
based on the time difference that an arbitrary vector would experience when transported over two differing spacetime paths. In Weyl's theory, the rate of a ticking
clock, as well as the total time difference, depends on the vector's past history. 
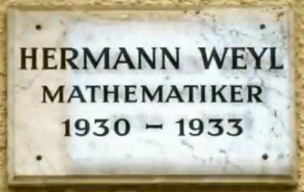 Here's an odd little
Here's an odd little

 Published in 1913 when the author was only 27, Hermann Weyl's first book was titled The Concept of a Riemann Surface
(you can download it legally for free
Published in 1913 when the author was only 27, Hermann Weyl's first book was titled The Concept of a Riemann Surface
(you can download it legally for free

 Leonard Susskind, the Felix Bloch Professor
of Physics at Stanford University, is one of the fathers of
string theory. Born to a poor Jewish family in the Bronx in 1940, he started out life as a plumber to help out his ailing father. The story goes that when he
told his father he wanted to be
an engineer, he was told "Hell no, you ain't gonna drive no train!" When Susskind decided later that he wanted to be a physicist, his father replied "Hell no, you ain't gonna work in
no drug store!" Another story tells about his being stuck in an elevator in 1968 with Caltech's Nobel Laureate Murray Gell-Mann. When asked idly what he was working on, Susskind
replied that he was studying the possibility that particles may actually be tiny Planck-sized strings, at which point Gell-Mann laughed riotously at such a silly idea.
Leonard Susskind, the Felix Bloch Professor
of Physics at Stanford University, is one of the fathers of
string theory. Born to a poor Jewish family in the Bronx in 1940, he started out life as a plumber to help out his ailing father. The story goes that when he
told his father he wanted to be
an engineer, he was told "Hell no, you ain't gonna drive no train!" When Susskind decided later that he wanted to be a physicist, his father replied "Hell no, you ain't gonna work in
no drug store!" Another story tells about his being stuck in an elevator in 1968 with Caltech's Nobel Laureate Murray Gell-Mann. When asked idly what he was working on, Susskind
replied that he was studying the possibility that particles may actually be tiny Planck-sized strings, at which point Gell-Mann laughed riotously at such a silly idea. 
 Sorry for this long post. I adapted it from a high school article I wrote in 2008.
Sorry for this long post. I adapted it from a high school article I wrote in 2008.  I really have nothing to do today.
I really have nothing to do today.  I've been in a political mood lately, so I'm not to be messed with.
I've been in a political mood lately, so I'm not to be messed with. 
 The spelling's off, true (and they struggled with the word 'impossible'), but the Tea Partier who displayed this sign in Washington last week got the sentiment right—the federal 1040 return process is in desperate need of reform (unless your income is as pathetic as mine, in which case the 1040 EZ for Dummies can be used). Hermann Weyl, upon becoming an American citizen after leaving Germany for Princeton in late 1933, said as much himself:
The spelling's off, true (and they struggled with the word 'impossible'), but the Tea Partier who displayed this sign in Washington last week got the sentiment right—the federal 1040 return process is in desperate need of reform (unless your income is as pathetic as mine, in which case the 1040 EZ for Dummies can be used). Hermann Weyl, upon becoming an American citizen after leaving Germany for Princeton in late 1933, said as much himself:
 Lincoln at Antietam battlefield, October 1862. At 6 feet 4 inches, he was our tallest Chief Executive.
Lincoln at Antietam battlefield, October 1862. At 6 feet 4 inches, he was our tallest Chief Executive. A nice photo of a young Hermann Weyl, undated but probably 1913
A nice photo of a young Hermann Weyl, undated but probably 1913 

 A lot of research is being conducted today regarding the dark matter (DM) and dark energy (DE) problems. It would appear to many researchers that these issues cannot be resolved by considering DM and DE to be merely some geometrical consequence of Einstein's general relativity (GR), so attention has been focused on the possible existence of new fields, with GR acting as a space-time bystander. Just what these fields may be no-one knows, but hypothetical critters like weakly-interacting massive particles (WIMPS) and new kinds of neutrinos have been suggested.
A lot of research is being conducted today regarding the dark matter (DM) and dark energy (DE) problems. It would appear to many researchers that these issues cannot be resolved by considering DM and DE to be merely some geometrical consequence of Einstein's general relativity (GR), so attention has been focused on the possible existence of new fields, with GR acting as a space-time bystander. Just what these fields may be no-one knows, but hypothetical critters like weakly-interacting massive particles (WIMPS) and new kinds of neutrinos have been suggested.  In 1921 Hermann Weyl offered this opinion in his Nature article entitled "Electricity and gravitation." Today, 91 years later, we still do not know whether Weyl was being ignorant, näive or extraordinarily prescient. Five years after he made this claim, physicists began to realize that there were more than just two fundamental forces; today we know there are four. Actually, it's only three—the electroweak theory is supposed to have unified the weak nuclear and electromagnetic forces, though this fact is often neglected when discussions of the fundamental forces of nature are brought up. And now there's evidence that gravity may in fact be describable in terms of the strong nuclear force, reducing the total back down to two, as Weyl surmised.
In 1921 Hermann Weyl offered this opinion in his Nature article entitled "Electricity and gravitation." Today, 91 years later, we still do not know whether Weyl was being ignorant, näive or extraordinarily prescient. Five years after he made this claim, physicists began to realize that there were more than just two fundamental forces; today we know there are four. Actually, it's only three—the electroweak theory is supposed to have unified the weak nuclear and electromagnetic forces, though this fact is often neglected when discussions of the fundamental forces of nature are brought up. And now there's evidence that gravity may in fact be describable in terms of the strong nuclear force, reducing the total back down to two, as Weyl surmised.  I was in Vienna, Austria recently and visited the city's Kaisergruft (Kaiser crypt), the underground mausoleum where Emperor Franz Josef and his family are entombed. Vienna seems to have a strange fascination with death, and I don't really know why—perhaps it has something to do with the world wars, both of which devastated the city. At any rate, the crypt has about 150 people buried here in unbelievably ornate, above-ground bronze caskets, each weighing tons. They're truly works of art, with macabre simulated bones and skulls and such, and they all reflect the enormous wealth associated with the dead. Most are full burials, while some containers hold only the hearts of the deceased. Like I say, it's strange.
I was in Vienna, Austria recently and visited the city's Kaisergruft (Kaiser crypt), the underground mausoleum where Emperor Franz Josef and his family are entombed. Vienna seems to have a strange fascination with death, and I don't really know why—perhaps it has something to do with the world wars, both of which devastated the city. At any rate, the crypt has about 150 people buried here in unbelievably ornate, above-ground bronze caskets, each weighing tons. They're truly works of art, with macabre simulated bones and skulls and such, and they all reflect the enormous wealth associated with the dead. Most are full burials, while some containers hold only the hearts of the deceased. Like I say, it's strange. 
 I finally acquired the 4-volume set of Hermann Weyl's Gessammelte Abhandlungen (literally, "collected essays"), which includes papers written by Weyl from his immediate post-PhD days (1910) to shortly before his death in 1955. I was pleasantly surprised that not all of the papers are in German (I can read the ones in physics alright, but the math papers are a real bitch); some are in English, a few in French (which I can read), and fewer still are in Spanish (shame on me, I never learned the language, and every Californian should know it). Altogether it's around 3,500 pages, but of course I'm only interested in the physics articles, many of which give a keen insight into the the mind of Weyl and his physics.
I finally acquired the 4-volume set of Hermann Weyl's Gessammelte Abhandlungen (literally, "collected essays"), which includes papers written by Weyl from his immediate post-PhD days (1910) to shortly before his death in 1955. I was pleasantly surprised that not all of the papers are in German (I can read the ones in physics alright, but the math papers are a real bitch); some are in English, a few in French (which I can read), and fewer still are in Spanish (shame on me, I never learned the language, and every Californian should know it). Altogether it's around 3,500 pages, but of course I'm only interested in the physics articles, many of which give a keen insight into the the mind of Weyl and his physics. 

 As we await the Supreme Court's politically-motivated decision to strike down health care
as we know it in this country and set the stage for a Romney or Santorum win in November, it's nice to know that there are good medical books out there to
help with the self-diagnoses and treatments we'll soon all be performing on ourselves.
As we await the Supreme Court's politically-motivated decision to strike down health care
as we know it in this country and set the stage for a Romney or Santorum win in November, it's nice to know that there are good medical books out there to
help with the self-diagnoses and treatments we'll soon all be performing on ourselves.
 So what's a sigma? It's one standard deviation of area under the unit-area curve
\( (2\pi)^{-0.5} \exp (-0.5 z^2) \), or about 0.68 (68%). 2-sigma corresponds to about 95%, which is what the LHC was reporting two months ago for the Higgs. So is 99.996% more or less a certainty that the Higgs has been discovered? Not at all, because scientists typically want 5 sigmas (about 99.9999%) before they're willing to announce anything. That's a figure that corresponds
to an uncertainty of less than one part in a million.
So what's a sigma? It's one standard deviation of area under the unit-area curve
\( (2\pi)^{-0.5} \exp (-0.5 z^2) \), or about 0.68 (68%). 2-sigma corresponds to about 95%, which is what the LHC was reporting two months ago for the Higgs. So is 99.996% more or less a certainty that the Higgs has been discovered? Not at all, because scientists typically want 5 sigmas (about 99.9999%) before they're willing to announce anything. That's a figure that corresponds
to an uncertainty of less than one part in a million. Some months ago I posted an article about Arizona State University's Lawrence Krauss, the astrophysicist who is the author of eight books, including The Physics of Star Trek (which I didn't much care for). He's now got another, far better book out called
Some months ago I posted an article about Arizona State University's Lawrence Krauss, the astrophysicist who is the author of eight books, including The Physics of Star Trek (which I didn't much care for). He's now got another, far better book out called
 It has been brought to my attention that on one or two occasions I have confused the German mathematician Paul Gordan (1837-1912, shown) with the German physicist Walter Gordon (1893-1939). To set the record straight, Paul Gordan was the PhD advisor to another noted German mathematician, Emmy Noether, and it was Gordan who worked with (yes, another noted German mathematician) Rudolf Clebsch to produce the Clebsch-Gordan coefficients (which no sane physics student enjoys learning about or using). It was the German physicist Walter Gordon who worked with the Swedish physicist Oskar Klein to produce the famous Klein-Gordon equation in 1925. Please make a note of it!
It has been brought to my attention that on one or two occasions I have confused the German mathematician Paul Gordan (1837-1912, shown) with the German physicist Walter Gordon (1893-1939). To set the record straight, Paul Gordan was the PhD advisor to another noted German mathematician, Emmy Noether, and it was Gordan who worked with (yes, another noted German mathematician) Rudolf Clebsch to produce the Clebsch-Gordan coefficients (which no sane physics student enjoys learning about or using). It was the German physicist Walter Gordon who worked with the Swedish physicist Oskar Klein to produce the famous Klein-Gordon equation in 1925. Please make a note of it!